题目内容
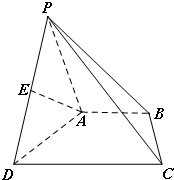 如图,在四棱锥P-ABCD中,BA⊥平面PAD,AP=AD,DC∥AB,DC=2AB,E是棱
如图,在四棱锥P-ABCD中,BA⊥平面PAD,AP=AD,DC∥AB,DC=2AB,E是棱PD的中点.
(1)求证:AE∥平面PBC;
(2)求证:平面PBC⊥平面PDC.
考点:平面与平面垂直的判定
专题:空间位置关系与距离
分析:(1)取PC中点F,连结BF,EF.由三角线中位线定理得四边形ABFE为平行四边形,由此能证明AE∥平面PBC.
(2)由等腰三角形性质得AE⊥PD.由AB⊥平面PAD,DC∥AB,得DC⊥AE.从而推导出BF⊥平面PCD.由此能证明平面PBC⊥平面PDC.
(2)由等腰三角形性质得AE⊥PD.由AB⊥平面PAD,DC∥AB,得DC⊥AE.从而推导出BF⊥平面PCD.由此能证明平面PBC⊥平面PDC.
解答:
证明:(1)取PC中点F,连结BF,EF.
 因为点E、F分别为棱PD、PC的中点,
因为点E、F分别为棱PD、PC的中点,
所以EF∥DC,且EF=
DC.
又AB∥DC,且AB=
DC,所以EF∥AB,且EF=AB.
于是,四边形ABFE为平行四边形,故有AE∥BF.
又因为AE不包含于平面PBC,BF?平面PBC,
所以AE∥平面PBC.…(6分)
(2)在△PAD中,因为AP=AD,且E为PD的中点,
所以AE⊥PD.因为AB⊥平面PAD,DC∥AB,
所以DC⊥平面PAD.又AE?平面PAD,所以DC⊥AE.
因为AE⊥PD,DC⊥AE,PD∩DC=D,PD、DC?平面PCD,
所以AE⊥平面PCD.又BF∥AE,所以BF⊥平面PCD.
又因为BF?平面PBC,所以平面PBC⊥平面PDC.…(12分)
 因为点E、F分别为棱PD、PC的中点,
因为点E、F分别为棱PD、PC的中点,所以EF∥DC,且EF=
| 1 |
| 2 |
又AB∥DC,且AB=
| 1 |
| 2 |
于是,四边形ABFE为平行四边形,故有AE∥BF.
又因为AE不包含于平面PBC,BF?平面PBC,
所以AE∥平面PBC.…(6分)
(2)在△PAD中,因为AP=AD,且E为PD的中点,
所以AE⊥PD.因为AB⊥平面PAD,DC∥AB,
所以DC⊥平面PAD.又AE?平面PAD,所以DC⊥AE.
因为AE⊥PD,DC⊥AE,PD∩DC=D,PD、DC?平面PCD,
所以AE⊥平面PCD.又BF∥AE,所以BF⊥平面PCD.
又因为BF?平面PBC,所以平面PBC⊥平面PDC.…(12分)
点评:本题考查直线与平面平行的证明,考查平面与平面垂直的证明,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目