题目内容
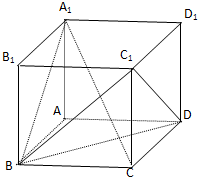 如图,正方体ABCD-A1B1C1D1的棱长为1.
如图,正方体ABCD-A1B1C1D1的棱长为1.(1)求异面直线BA1与CC1所成角的大小;
(2)求证:A1C⊥平面BC1D;
(3)求三棱锥C-BDC1的表面积.
考点:棱柱、棱锥、棱台的体积,异面直线及其所成的角,直线与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(1)因为BB1与CC1平行,所以将CC1平移到BB1,从而∠B1BA1为直线BA1和CC1所成的角,在三角形A1BB1中易求;
(2)要证明A1C⊥平面BC1D,只需证明直线A1C垂直于平面BC1D内的两条相交直线即可,故只需证明A1C⊥BD,A1C⊥BC1即可;
(3)利用侧面积加上底面积,即可求三棱锥C-BDC1的表面积.
(2)要证明A1C⊥平面BC1D,只需证明直线A1C垂直于平面BC1D内的两条相交直线即可,故只需证明A1C⊥BD,A1C⊥BC1即可;
(3)利用侧面积加上底面积,即可求三棱锥C-BDC1的表面积.
解答:
 (1)解:∵BB1∥CC1
(1)解:∵BB1∥CC1
∴∠B1BA1为直线BA1和CC1所成的角,
∵四边形AA1B1B是正方形
∴△B1BA1为等腰直角三角形
∴∠B1BA1=45°,即直线BA1和CC1所成的角为45°-----------(4分)
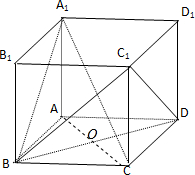
(2)证明:连接AC交BD于一点O,
在正方形ABCD中,BD⊥AC,
又正方体中,AA1⊥平面ABCD,
所以,AA1⊥BD,又AA1∩AC=A,
所以BD⊥平面CAA1又A1C?平面CAA1
所以A1C⊥BD,
同理可证A1C⊥BC1,又 BC1交BD于一点B,
所以A1C⊥平面BC1D(10分)
(3)解:三棱锥C-BDC1的表面积为3•
•1•1+
•(
)2=
----------------------(14分)
 (1)解:∵BB1∥CC1
(1)解:∵BB1∥CC1∴∠B1BA1为直线BA1和CC1所成的角,
∵四边形AA1B1B是正方形
∴△B1BA1为等腰直角三角形
∴∠B1BA1=45°,即直线BA1和CC1所成的角为45°-----------(4分)
(2)证明:连接AC交BD于一点O,
在正方形ABCD中,BD⊥AC,
又正方体中,AA1⊥平面ABCD,
所以,AA1⊥BD,又AA1∩AC=A,
所以BD⊥平面CAA1又A1C?平面CAA1
所以A1C⊥BD,
同理可证A1C⊥BC1,又 BC1交BD于一点B,
所以A1C⊥平面BC1D(10分)
(3)解:三棱锥C-BDC1的表面积为3•
| 1 |
| 2 |
| ||
| 4 |
| 2 |
3+
| ||
| 2 |
点评:本题着重考查了异面直线的判定,直线与平面位置关系中的垂直问题,证明思路是:要证线面垂直,需证线线垂直,在证明线线垂直过程中,往往需要通过证明线面垂直来实现,要注意线面垂直、线线垂直间的相互转化.

练习册系列答案
相关题目