题目内容
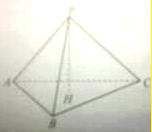 如图,P为△ABC所在平面外一点,PA⊥PB,PB⊥PC,PC⊥PA,PH⊥平面ABC于H,求证:H是△ABC的垂心,△ABC为锐角三角形.
如图,P为△ABC所在平面外一点,PA⊥PB,PB⊥PC,PC⊥PA,PH⊥平面ABC于H,求证:H是△ABC的垂心,△ABC为锐角三角形.考点:直线与平面垂直的性质
专题:证明题
分析:(1),由三条侧棱PA,PB,PC两两垂直可以得到PA⊥面PBC,进而得到PA⊥BC,由PH⊥平面ABC于H,BC?面ABC,可得PH⊥BC,故BC⊥平面APE,从而有AE?面APE,即可得∴BC⊥AE;同理可以证明才CH⊥AB,又BH⊥AC.即可证明H是△ABC的垂心.
(2),可以通过余弦定理解决.
(2),可以通过余弦定理解决.
解答:
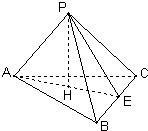 证明:(1)连接AH并延长交BC于一点E,连接PH,由于PA,PB,PC两两垂直可以得到PA⊥面PBC,而BC?面PBC,∴BC⊥PA,
证明:(1)连接AH并延长交BC于一点E,连接PH,由于PA,PB,PC两两垂直可以得到PA⊥面PBC,而BC?面PBC,∴BC⊥PA,
∵PH⊥平面ABC于H,BC?面ABC,∴PH⊥BC,∴BC⊥平面APE,∵AE?面APE,
∴BC⊥AE;
同理可以证明才CH⊥AB,又BH⊥AC.
∴H是△ABC的垂心.
(2)设PA=a;PB=b;PC=c,则AB2=a2+b2,同理BC2=c2+b2,Ac2=a2+c2,在三角形ABC中,由余弦定理得:cosA=
=
=
>0,同理可证cosB>0,cosC>0,所以,△ABC是锐角三角形.
 证明:(1)连接AH并延长交BC于一点E,连接PH,由于PA,PB,PC两两垂直可以得到PA⊥面PBC,而BC?面PBC,∴BC⊥PA,
证明:(1)连接AH并延长交BC于一点E,连接PH,由于PA,PB,PC两两垂直可以得到PA⊥面PBC,而BC?面PBC,∴BC⊥PA,∵PH⊥平面ABC于H,BC?面ABC,∴PH⊥BC,∴BC⊥平面APE,∵AE?面APE,
∴BC⊥AE;
同理可以证明才CH⊥AB,又BH⊥AC.
∴H是△ABC的垂心.
(2)设PA=a;PB=b;PC=c,则AB2=a2+b2,同理BC2=c2+b2,Ac2=a2+c2,在三角形ABC中,由余弦定理得:cosA=
| AB2+AC2-BC2 |
| 2×AB×AC |
| a2+b2+a2+c2-c2-b2 | ||||
2
|
| a2 | ||||
|
点评:本题考查直线与平面垂直的证明法:利用判定定理证明;以及解三角形的有关理论,第二问在立体几何中考查平面几何问题,要注意在空间的某个平面内,平面几何的有关定理、公式等结论仍然成立,属于基本知识的考查.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知命题p:若2b=a+c,则a、b、c成等差数列;命题q:若b2=ac,则a、b、c成等比数列,则下列命题中是真命题的是( )
| A、¬p或q | B、p且q |
| C、¬p且¬q | D、¬p或¬q |
已知曲线C:f(x)=x3-ax+a,若过曲线C外一点A(1,0)引曲线C的两条切线,它们的倾斜角互补,则a的值为( )
A、
| ||
| B、-2 | ||
| C、2 | ||
D、-
|
设Sn为等比数列{an}的前n项和,S4=1,S8=3,则S20=( )
| A、15 | B、16 | C、81 | D、31 |