题目内容
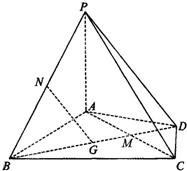 在四棱锥P-ABCD中,PA⊥平面ABCD,AD⊥AB,△ABC是正三角形,AC与BD的交点M恰好是AC中点,N为线段PB的中点,G在线段BM上,且
在四棱锥P-ABCD中,PA⊥平面ABCD,AD⊥AB,△ABC是正三角形,AC与BD的交点M恰好是AC中点,N为线段PB的中点,G在线段BM上,且| BG |
| GM |
(Ⅰ)求证:AB⊥PD;
(Ⅱ)求证:GN∥平面PCD.
考点:直线与平面平行的判定
专题:
分析:(Ⅰ)根据线面垂直的性质和判定,即可得证;
(Ⅱ)由等边三角形的性质和直角三角形中30°所对的直角边为斜边的一半,得到MD=
BD,由平行线分线段成比例的判定得到GN∥PD,再由线面平行的判定定理即可得证.
(Ⅱ)由等边三角形的性质和直角三角形中30°所对的直角边为斜边的一半,得到MD=
| 1 |
| 4 |
解答:
(Ⅰ)证明:∵PA⊥平面ABCD,
∴PA⊥AB,
又∵AD⊥AB,∴AB⊥平面PAD,
又PD?平面PAD,∴AB⊥PD.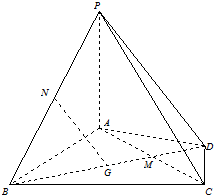
(Ⅱ)证明:∵△ABC是正三角形,且M是AC中点,
∴BM⊥AC,
在直角三角形AMD中,∠MAD=30°,∴MD=
AD,
在直角三角形ABD中,∠ABD=30°,∴AD=
BD,
∴MD=
BD,
又∵
=2,∴BG=GD,又N为线段PB的中点,
∴GN∥PD,GN?平面PCD,PD?平面PCD,
∴GN∥平面PCD.
∴PA⊥AB,
又∵AD⊥AB,∴AB⊥平面PAD,
又PD?平面PAD,∴AB⊥PD.

(Ⅱ)证明:∵△ABC是正三角形,且M是AC中点,
∴BM⊥AC,
在直角三角形AMD中,∠MAD=30°,∴MD=
| 1 |
| 2 |
在直角三角形ABD中,∠ABD=30°,∴AD=
| 1 |
| 2 |
∴MD=
| 1 |
| 4 |
又∵
| BG |
| GM |
∴GN∥PD,GN?平面PCD,PD?平面PCD,
∴GN∥平面PCD.
点评:本题主要考查线面垂直的判定和性质,以及线面平行的判定定理,注意线线垂直与线面垂直的相互转化,本题属于基础题.

练习册系列答案
相关题目
 如图所示,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,
如图所示,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,