题目内容
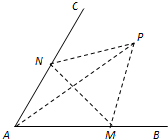 如图,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N (异于村庄A),要求PM=PN=MN=2(单位:千米).设∠AMN=θ.
如图,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N (异于村庄A),要求PM=PN=MN=2(单位:千米).设∠AMN=θ.(1)在△AMN和△AMP中试用θ表示AM和AP2;
(2)设AP2=f(θ),化简f(θ);
(3)θ为多少时,工厂产生的噪声对居民的影响最小(即工厂与村庄的距离AP最远),并求出AP的最大值.
考点:正弦定理的应用
专题:解三角形
分析:(1)根据正弦定理,即可θ表示AM和AP2;
(2)设AP2=f(θ),根据三角函数的公式,以及辅助角公式即可化简f(θ);
(3)根据三角函数的图象和性质,即可求出函数的最值.
(2)设AP2=f(θ),根据三角函数的公式,以及辅助角公式即可化简f(θ);
(3)根据三角函数的图象和性质,即可求出函数的最值.
解答:
解:(1)∠AMN=θ,在△AMN中,
=
.
因为MN=2,所以AM=
sin(120°-θ). …(2分)
在△APM中,cos∠AMP=cos(60°+θ). …(5分)
AP2=AM2+MP2-2 AM•MP•cos∠AMP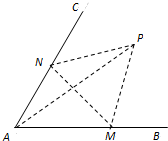
=
sin2(120°-θ)+4-2×2×
sin(120°-θ) cos(60°+θ) …(7分)
=
sin2(θ+60°)-
sin(θ+60°) cos(θ+60°)+4
=
[1-cos (2θ+120°)]-
sin(2θ+120°)+4
=-
[
sin(2θ+120°)+cos (2θ+120°)]+
=
-
sin(2θ+150°),θ∈(0,120°). …(11分)
当且仅当2θ+150°=270°,即θ=60°时,AP2取得最大值12,即AP取得最大值2
.
答:设计∠AMN为60°时,工厂产生的噪声对居民的影响最小.…(13分)
| MN |
| sin60° |
| AM |
| sin(120°-θ) |
因为MN=2,所以AM=
4
| ||
| 3 |
在△APM中,cos∠AMP=cos(60°+θ). …(5分)
AP2=AM2+MP2-2 AM•MP•cos∠AMP

=
| 16 |
| 3 |
4
| ||
| 3 |
=
| 16 |
| 3 |
16
| ||
| 3 |
=
| 8 |
| 3 |
8
| ||
| 3 |
=-
| 8 |
| 3 |
| 3 |
| 20 |
| 3 |
=
| 20 |
| 3 |
| 16 |
| 3 |
当且仅当2θ+150°=270°,即θ=60°时,AP2取得最大值12,即AP取得最大值2
| 3 |
答:设计∠AMN为60°时,工厂产生的噪声对居民的影响最小.…(13分)
点评:本题主要考查与三角函数有关的应用问题,利用正弦定理以及三角函数的三角公式是解决本题的关键.

练习册系列答案
相关题目
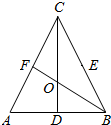 在△ABC中,D、E、F分别是AB、BC、CA的中点,BF与CD交于点O,设向量
在△ABC中,D、E、F分别是AB、BC、CA的中点,BF与CD交于点O,设向量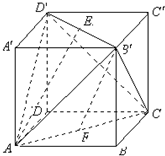 正方体ABCD-A′B′C′D′的棱长等于2,E,F分别是B′D′,AC的中点.求:
正方体ABCD-A′B′C′D′的棱长等于2,E,F分别是B′D′,AC的中点.求: