题目内容
(1)平面α过坐标原点O,
=(1,2,3)是平面α的一个法向量,求P(-1,2,0)到平面α的距离;
(2)直线l过A(2,2,1),
=(-1,0,1)是直线l的一个方向向量,求P(0,2,2)到直线l的距离.
| n |
(2)直线l过A(2,2,1),
| s |
考点:点、线、面间的距离计算
专题:综合题,空间位置关系与距离
分析:(1)设点P到平面OAB的距离为d,则d=
,可求P(-1,2,0)到平面α的距离;
(2)求出
与直线l的方向向量的夹角的正弦,即可求P(0,2,2)到直线l的距离.
|
| ||||
|
|
(2)求出
| AP |
解答:
解:(1)设P到平面α的距离为d,d=
=
=
;
(2)由题意,
=(-2,0,1),
∴
与直线l的方向向量的夹角的余弦为
=
,
∴
与直线l的方向向量的夹角的正弦为
,
∵|
|=
,
∴P到直线l的距离为
.
|
| ||||
|
|
| |(-1,2,0)•(1,2,3)| | ||
|
3
| ||
| 14 |
(2)由题意,
| AP |
∴
| AP |
| 3 | ||||
|
| 3 | ||
|
∴
| AP |
| 1 | ||
|
∵|
| AP |
| 5 |
∴P到直线l的距离为
| ||
| 2 |
点评:本题考查利用空间向量求点面距离、点线距离,利用点P到平面OAB的距离为d,则d=
是解题的关键.
|
| ||||
|
|

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案
相关题目
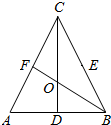 在△ABC中,D、E、F分别是AB、BC、CA的中点,BF与CD交于点O,设向量
在△ABC中,D、E、F分别是AB、BC、CA的中点,BF与CD交于点O,设向量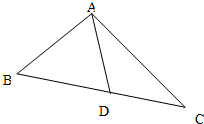 如图,在△ABC中,已知∠B=45°,D是BC边上的一点,AD=10,AC=14,DC=6.
如图,在△ABC中,已知∠B=45°,D是BC边上的一点,AD=10,AC=14,DC=6.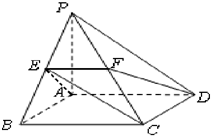 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AB=AP=2,AD=4,E、F依次是PB、PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AB=AP=2,AD=4,E、F依次是PB、PC的中点.