题目内容
已知直线l的参数方程为
(t为参数),以坐标原点O为极点,x轴的正半轴为极轴简历极坐标系,曲线C的极坐标方程为ρ2cos2θ=-2.
(1)把直线l的参数方程化为极坐标方程;
(2)若直线l交曲线C于A(ρ1,θ1),B(ρ2,θ2)两点,求ρ12ρ22的值.
|
(1)把直线l的参数方程化为极坐标方程;
(2)若直线l交曲线C于A(ρ1,θ1),B(ρ2,θ2)两点,求ρ12ρ22的值.
考点:参数方程化成普通方程
专题:选作题,坐标系和参数方程
分析:(1)利用极坐标与直角坐标之间的关系即可得出其极坐标方程;
(2)ρ2cos2θ=-2的直角坐标方程为x2-y2=-2,与
x-y-2
=0联立,求出A,B的坐标,即可求ρ12ρ22的值.
(2)ρ2cos2θ=-2的直角坐标方程为x2-y2=-2,与
| 3 |
| 3 |
解答:
解:(1)直线l的参数方程为
(t为参数),普通方程为
x-y-2
=0,
将ρcosθ=x,ρsinθ=y代入可得
ρcosθ-ρsinθ-2
=0;
(2)ρ2cos2θ=-2的直角坐标方程为x2-y2=-2,
与
x-y-2
=0联立可得x2-6x+5=0,
∴x=1或5,
∴A(1,-
),B(5,3
),
∴ρ12ρ22=(1+3)(25+27)=208.
|
| 3 |
| 3 |
将ρcosθ=x,ρsinθ=y代入可得
| 3 |
| 3 |
(2)ρ2cos2θ=-2的直角坐标方程为x2-y2=-2,
与
| 3 |
| 3 |
∴x=1或5,
∴A(1,-
| 3 |
| 3 |
∴ρ12ρ22=(1+3)(25+27)=208.
点评:本题考查点的极坐标和直角坐标的互化,以及利用平面几何知识解决最值问题.利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得.

练习册系列答案
相关题目
已知幂函数y=f(x)的图象过点(2,
),则f(log216)=( )
| 2 |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
设X为随机变量,X~B(n,
),若随机变量X的方差D(X)=1,则P(X=2)等于( )
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
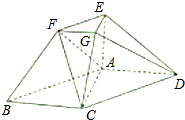 在如图所示的几何体中,ABCD为平行四边形,∠ACB=
在如图所示的几何体中,ABCD为平行四边形,∠ACB=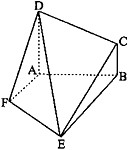 如图,四边形ABCD和ABEF都是直角梯形,AD∥BC,AF∥BE,∠DAB=∠FAB=90°,且平面ABCD⊥平面ABEF,DA=AB=BE=2,BC=1.
如图,四边形ABCD和ABEF都是直角梯形,AD∥BC,AF∥BE,∠DAB=∠FAB=90°,且平面ABCD⊥平面ABEF,DA=AB=BE=2,BC=1.