题目内容
若a>0,a≠1,且m>0,n>0,则下列各式中正确的是( )
| A、logam•logan=loga(m+n) | ||||||||||
| B、am•an=am•n | ||||||||||
C、
| ||||||||||
| D、1÷an=a0-n |
考点:对数的运算性质
专题:函数的性质及应用
分析:由对数式的运算性质排除A,C;由指数式的运算性质排除B;再由指数式的运算性质验证D得答案.
解答:
解:由对数的运算性质可知A,C错误;
由am•an=am+n可知C错误;
1÷an=a0÷an=a0-n,
∴D正确.
故选:D.
由am•an=am+n可知C错误;
1÷an=a0÷an=a0-n,
∴D正确.
故选:D.
点评:本题考查了指数的运算性质和对数的运算性质,是基础题.

练习册系列答案
相关题目
下列说法正确的是( )
| A、“a>b”是“a2>b2”的必要条件 | ||
| B、“若a,b都是偶数,则a+b是偶数”的否命题为真 | ||
C、若x,y∈R,则“x=y”是“xy≤(
| ||
| D、已知命题p,q,若(¬p)∨q为假命题,则p∧(¬q)为真命题 |
函数y=
的定义域为( )
| 1 |
| log2(x-1) |
| A、(-∞,1) |
| B、(1,+∞) |
| C、(1,2)∪(2,+∞) |
| D、(1,3)∪(3,+∞) |
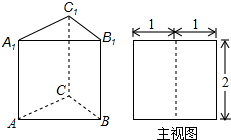 如图,三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,且侧棱AA1⊥底面ABC,其主视图是边长为2的正方形,则此三棱柱左视图的面积为( )
如图,三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,且侧棱AA1⊥底面ABC,其主视图是边长为2的正方形,则此三棱柱左视图的面积为( )