题目内容
求下列函数的导数:y=ln(2x+3)+x2.
考点:导数的运算
专题:导数的综合应用
分析:直接利用和的导数等于导数的和,然后利用简单的复合函数求导得答案.
解答:
解:∵y=ln(2x+3)+x2,
∴y′=
•(2x+3)′+2x
=
+2x.
∴y′=
| 1 |
| 2x+3 |
=
| 2 |
| 2x+3 |
点评:本题考查了简单的复合函数的导数,考查了基本初等函数的导数公式,是基础题.

练习册系列答案
相关题目
当a≠0时,函数y=ax+b和函数y=bax的图象可能是( )
A、 |
B、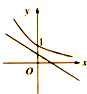 |
C、 |
D、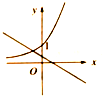 |
若a>0,a≠1,且m>0,n>0,则下列各式中正确的是( )
| A、logam•logan=loga(m+n) | ||||||||||
| B、am•an=am•n | ||||||||||
C、
| ||||||||||
| D、1÷an=a0-n |
在△ABC中,a=4,b=6,A=30°,则sinB=( )
A、
| ||
B、
| ||
C、
| ||
D、
|