题目内容
函数y=
的定义域为（ ）
| 1 |
| log2(x-1) |
| A、（-∞，1） |
| B、（1，+∞） |
| C、（1，2）∪（2，+∞） |
| D、（1，3）∪（3，+∞） |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：对数函数的真数大于0，且分母不等于0，列出不等式组，求出解集即可；
解答：
解：要使函数有意义，x需满足：
，
∴
，解得x＞1，且x≠2，
故函数的定义域为（1，2）∪（2，+∞），
故选：C．
|
∴
|
故函数的定义域为（1，2）∪（2，+∞），
故选：C．
点评：本题考查了求函数定义域的问题，即求使函数解析式有意义的自变量的取值范围，是基础题目．
练习册系列答案
阅读快车系列答案
相关题目
若a＞0，a≠1，且m＞0，n＞0，则下列各式中正确的是（ ）
| A、logam•logan=loga（m+n） | ||||||||||
| B、am•an=am•n | ||||||||||
C、
| ||||||||||
| D、1÷an=a0-n |
y=2sin（
x-
）的周期为（ ）
| 1 |
| 2 |
| π |
| 6 |
A、
| ||
| B、π | ||
| C、2π | ||
| D、4π |
已知全集U={1，2，3，4}，集合A={1，2，4}，B={2，3}，则图中阴影部分表示的集合为（ ）| A、{2} |
| B、{3} |
| C、{1，4} |
| D、{1，2，3，4} |
如图所示，四边形ABEF和ABCD都是直角梯形，∠BAD=∠FAB=90°，BC
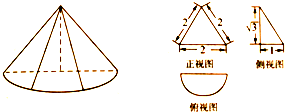已知图（2）是图（1）所示几何体的三视图，其中俯视图是个半圆，则图（1）所示几何体的表面积为（ ）A、
| ||||
B、π+
| ||||
C、
| ||||
D、
|
已知直线m，n和平面α，β，若α⊥β，α∩β=m，n?α，要使n⊥β，则应增加的条件是（ ）
| A、m∥n | B、n∥α |
| C、n⊥m | D、n⊥α |