题目内容
14.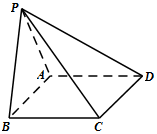 如图,四棱锥P-ABCD的底面ABCD为平行四边形,平面PAB⊥平面ABCD,PB=PC,∠ABC=45°.
如图,四棱锥P-ABCD的底面ABCD为平行四边形,平面PAB⊥平面ABCD,PB=PC,∠ABC=45°.(Ⅰ)求证:AB⊥PC;
(Ⅱ)若三角形PAB是边长为2的等边三角形,求三棱锥P-ABC外接球的表面积.
分析 (Ⅰ)作PO⊥AB于O,连接OC,推导出PO⊥面ABCD.再求出OC⊥AB,从而AB⊥面POC,由此能证明AB⊥PC.
(Ⅱ)在线段PO上取点E,EA=EB=EC,E是外接球的球心,设三棱锥P-ABC外接球的半径为R,则EC2=EO2+OC2,由此能求出三棱锥P-ABC外接球的表面积.
解答 证明:(Ⅰ)作PO⊥AB于O…①,连接OC,
∵平面PAB⊥平面ABCD,且面PAB∩面ABCD=AB,
∴PO⊥面ABCD.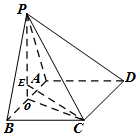
∵PB=PC,∴△POB≌△POC,∴OB=OC,
又∵∠ABC=45°,∴OC⊥AB…②
又PO∩CO=O,由①②,得AB⊥面POC,
又PC?面POC,∴AB⊥PC.…(6分)
解:(Ⅱ)∵三角形PAB是边长为2的等边三角形,
∴$PO=\sqrt{3},OA=OB=OC=1$.
∵PO⊥面ABCD,PO>OA=OB=OC,线段PO上取点E,
∴EA=EB=EC,E是外接球的球心,
设三棱锥P-ABC外接球的半径为R,
$EO=\sqrt{3}-R,EC=R$,EC2=EO2+OC2,
${R^2}={1^2}+{(\sqrt{3}-R)^2}$,$R=\frac{{2\sqrt{3}}}{3}$,
∴三棱锥P-ABC外接球的表面积$S=4π{R^2}=\frac{16π}{3}$.…(12分)
点评 本题考查线线垂直的证明,考查几何体的表面积的求法,考查空间中线线、线面、面面间的位置关系,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、数形结合思想、函数与方程思想是,是中档题.

练习册系列答案
相关题目
5.若$a={log_{\frac{1}{π}}}\frac{1}{3}$,$b={e^{\frac{π}{3}}}$,$c={log_3}cos\frac{1}{5}π$,则( )
| A. | b>c>a | B. | b>a>c | C. | a>b>c | D. | c>a>b |
9.已知函数f(x)=acosx+bx2+2(a∈R,b∈R),f'(x)为f(x)的导函数,则f(2016)-f(-2016)+f'(2017)+f'(-2017)=( )
| A. | 4034 | B. | 4032 | C. | 4 | D. | 0 |
13.已知正四面体的棱长为4,则此四面体的外接球的表面积是( )
| A. | 24π | B. | 18π | C. | 12π | D. | 6π |
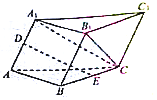 如图,在三棱柱ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,∠A1AC=60°,AC=2AA1=4,点D,E分别是AA1,BC的中点.
如图,在三棱柱ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,∠A1AC=60°,AC=2AA1=4,点D,E分别是AA1,BC的中点.