题目内容
2.对任意k∈[1,5],直线l:y=kx-k-1都与平面区域$\left\{\begin{array}{l}x≥a\\ x+y≤6\\ x-2y≤0\end{array}\right.$有公共点,则实数a的最大值是2.分析 由约束条件作出可行域,再由直线y=kx-k-1恒过定点,数形结合得答案.
解答 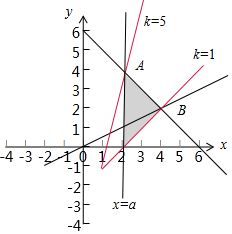 解:由不等式组$\left\{\begin{array}{l}x≥a\\ x+y≤6\\ x-2y≤0\end{array}\right.$作出可行域如图,而直线l:y=kx-k-1恒过定点P(1,-1),对任意k∈[1,5],直线l:y=kx-k-1都与平面区域$\left\{\begin{array}{l}x≥a\\ x+y≤6\\ x-2y≤0\end{array}\right.$有公共点,
解:由不等式组$\left\{\begin{array}{l}x≥a\\ x+y≤6\\ x-2y≤0\end{array}\right.$作出可行域如图,而直线l:y=kx-k-1恒过定点P(1,-1),对任意k∈[1,5],直线l:y=kx-k-1都与平面区域$\left\{\begin{array}{l}x≥a\\ x+y≤6\\ x-2y≤0\end{array}\right.$有公共点,
当k=5时,直线l:y=5x-6经过可行域的点A,
联立$\left\{\begin{array}{l}{x+y=6}\\{y=5x-6}\end{array}\right.$,解得A(2,5),
点A是直线x=a上的点,可得a的最大值是2.
故答案为:2.
点评 本题考查简单的线性规划,考查数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
12.若直线x=$\frac{5}{4}$π和x=$\frac{9}{4}$π是函数y=sin(ωx+φ)(ω>0)图象的两条相邻对称轴,则φ的一个可能取值为( )
| A. | $\frac{3π}{4}$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{4}$ |
13.设直角坐标平面内与两个定点A(-2,0),B(2,0)的距离之差的绝对值等于2的点的轨迹是E.过点B作与x轴垂直的直线l与曲线E交于C,D两点,则$\overrightarrow{AC}•\overrightarrow{BD}$=( )
| A. | -9 | B. | -3 | C. | 3 | D. | 9 |
7.已知集合A={x∈R|0<x≤5},B={x∈R|log2(2-x)<2},则(∁RB)∩A=( )
| A. | (-2,5] | B. | [-2,5] | C. | (2,5] | D. | [2,5] |
1.圆心在(1,0)且过极点的圆的极坐标方程为( )
| A. | ρ=1 | B. | ρ=cos θ | C. | ρ=2cos θ | D. | ρ=2sin θ |
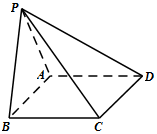 如图,四棱锥P-ABCD的底面ABCD为平行四边形,平面PAB⊥平面ABCD,PB=PC,∠ABC=45°.
如图,四棱锥P-ABCD的底面ABCD为平行四边形,平面PAB⊥平面ABCD,PB=PC,∠ABC=45°.