题目内容
13.已知正四面体的棱长为4,则此四面体的外接球的表面积是( )| A. | 24π | B. | 18π | C. | 12π | D. | 6π |
分析 将正四面体补成一个正方体,正四面体的外接球的直径为正方体的对角线长,即可得出结论.
解答 解:将正四面体补成一个正方体,则正方体的棱长为2$\sqrt{2}$,正方体的对角线长为2$\sqrt{6}$,
∵正四面体的外接球的直径为正方体的对角线长,外接球的半径为:$\sqrt{6}$,
∴外接球的表面积的值为4π•($\sqrt{6}$)2=24π.
故选:A.
点评 本题考查球的内接多面体等基础知识,考查运算求解能力,考查逻辑思维能力,属于基础题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
1.圆心在(1,0)且过极点的圆的极坐标方程为( )
| A. | ρ=1 | B. | ρ=cos θ | C. | ρ=2cos θ | D. | ρ=2sin θ |
8.掷两枚均匀的大小不同的骰子,记“两颗骰子的点数和为8”为事件A,“小骰子出现的点数小于大骰子出现的点数”为事件B,则P(A|B),P(B|A)分别为( )
| A. | $\frac{2}{15},\frac{2}{5}$ | B. | $\frac{3}{14},\frac{3}{5}$ | C. | $\frac{1}{3},\frac{1}{5}$ | D. | $\frac{4}{5},\frac{4}{15}$ |
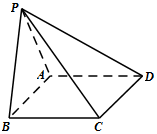 如图,四棱锥P-ABCD的底面ABCD为平行四边形,平面PAB⊥平面ABCD,PB=PC,∠ABC=45°.
如图,四棱锥P-ABCD的底面ABCD为平行四边形,平面PAB⊥平面ABCD,PB=PC,∠ABC=45°.