题目内容
9.已知函数f(x)=acosx+bx2+2(a∈R,b∈R),f'(x)为f(x)的导函数,则f(2016)-f(-2016)+f'(2017)+f'(-2017)=( )| A. | 4034 | B. | 4032 | C. | 4 | D. | 0 |
分析 根据题意,分析可得f(x)=acosx+bx2+2为偶函数,则有f(2016)-f(-2016)=0,对函数f(x)求导可得f′(x),分析可得f′(x)为奇函数,则有f'(2017)+f'(-2017)=0,将f(2016)-f(-2016)与f'(2017)+f'(-2017)相加即可得答案.
解答 解:根据题意,函数f(x)=acosx+bx2+2,f(-x)=acos(-x)+b(-x)2+2=f(x),
则函数f(x)为偶函数,
则有f(2016)=f(-2016),即f(2016)-f(-2016)=0,
函数f(x)=acosx+bx2+2,
则其导数f′(x)=-asinx+2bx,
又由f′(-x)=-asin(-x)+2b(-x)=-(-asinx+2bx)=-f′(x),
即函数f′(x)=-asinx+2bx为奇函数,
则有f'(2017)=-f'(-2017),即f'(2017)+f'(-2017)=0;
则f(2016)-f(-2016)+f'(2017)+f'(-2017)=0+0=0;
故选:D.
点评 本题考查导数的计算,涉及函数奇偶性的性质,关键是求出函数f(x)的导数并分析导函数的奇偶性.

练习册系列答案
相关题目
19.已知e为自然对数的底,a=($\frac{2}{e}$)-0.2,b=($\frac{e}{2}$)0.4,c=$lo{g}_{\frac{2}{e}}e$,则a,b,c的大小关系是( )
| A. | c<a<b | B. | c<b<a | C. | b<a<c | D. | a<b<c |
7.对具有线性相关关系的变量x,y有一组观测数据(xi,yi)(i=1,2,3,…,n),观测数据均在回归直线方程$y=\frac{1}{3}x+2$上,则该组数据的残差平方和的值为( )
| A. | 0 | B. | $\frac{1}{3}$ | C. | 1 | D. | 2 |
8.掷两枚均匀的大小不同的骰子,记“两颗骰子的点数和为8”为事件A,“小骰子出现的点数小于大骰子出现的点数”为事件B,则P(A|B),P(B|A)分别为( )
| A. | $\frac{2}{15},\frac{2}{5}$ | B. | $\frac{3}{14},\frac{3}{5}$ | C. | $\frac{1}{3},\frac{1}{5}$ | D. | $\frac{4}{5},\frac{4}{15}$ |
 如图,四棱锥P-ABCD的底面ABCD为平行四边形,平面PAB⊥平面ABCD,PB=PC,∠ABC=45°,点E是线段PA上靠近点A的三等分点.
如图,四棱锥P-ABCD的底面ABCD为平行四边形,平面PAB⊥平面ABCD,PB=PC,∠ABC=45°,点E是线段PA上靠近点A的三等分点.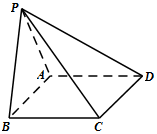 如图,四棱锥P-ABCD的底面ABCD为平行四边形,平面PAB⊥平面ABCD,PB=PC,∠ABC=45°.
如图,四棱锥P-ABCD的底面ABCD为平行四边形,平面PAB⊥平面ABCD,PB=PC,∠ABC=45°.