题目内容
定义在R上的奇函数f(x),满足f(1)=0,且在(0,+∞)上单调递增,则xf(x)>0的解集为( )
| A、{x|x<-1或x>1} |
| B、{x|0<x<1或-1<x<0} |
| C、{x|0<x<1或x<-1} |
| D、{x|-1<x<0或x>1} |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:先确定函数f(x)在(-∞,0)上单调递增,且f(-1)=0,再将不等式等价变形,即可得到结论.
解答:
解:∵定义在R上的奇函数f(x)在(0,+∞)上单调递增,且f(1)=0,
∴函数f(x)在(-∞,0)上单调递增,且f(-1)=0,
∴不等式xf(x)>0等价于
或
∴x>1或-1≤x<-1
∴不等式xf(x)>0的解集为{x|x>1或x<-1}.
故选A.
∴函数f(x)在(-∞,0)上单调递增,且f(-1)=0,
∴不等式xf(x)>0等价于
|
|
∴x>1或-1≤x<-1
∴不等式xf(x)>0的解集为{x|x>1或x<-1}.
故选A.
点评:本题考查函数单调性与奇偶性的结合,关键利用函数上奇函数得到对称区间得单调性,经常考查,属于基础题.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
已知f:x→x2是集合A到集合B={0,1,4}的一个映射,则集合A中的元素个数最多有( )
| A、3个 | B、4个 | C、5个 | D、6个 |
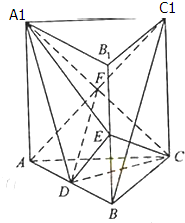 如图,三棱柱ABC-A1B1C1中,AA1⊥面ABC,D,E分别是AB,BB1的中点,AA1=AC=CB=4,AB=4
如图,三棱柱ABC-A1B1C1中,AA1⊥面ABC,D,E分别是AB,BB1的中点,AA1=AC=CB=4,AB=4