题目内容
在等差数列{an}中,a1=1,a2+a4=6.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)将数列{an}的前4项抽去其中一项后,剩下的三项构成公比大于1的等比数列{bn}的前三项,记数列{bn}前n项的和为Sn,若对任意n∈N*,使得Sn≥λ成立,求实数λ的取值范围.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)将数列{an}的前4项抽去其中一项后,剩下的三项构成公比大于1的等比数列{bn}的前三项,记数列{bn}前n项的和为Sn,若对任意n∈N*,使得Sn≥λ成立,求实数λ的取值范围.
考点:等差数列的性质
专题:计算题,等差数列与等比数列
分析:(Ⅰ)求出公差,即可求数列{an}的通项公式;
(Ⅱ)求出Sn,利用对任意n∈N*,使得Sn≥λ成立,即可求实数λ的取值范围.
(Ⅱ)求出Sn,利用对任意n∈N*,使得Sn≥λ成立,即可求实数λ的取值范围.
解答:
解:(Ⅰ)设公差为d,则由a1=1,2a1+4d=6得d=1,
∴an=n…(5分)
(Ⅱ)由(Ⅰ)得a1=1,a2=2,a3=3,a4=4
而{bn}是公比大于1的等比数列,
∴b1=1,b2=2,b3=4,∴q=2…(8分)
∴Sn=
=2n-1,
又对任意n∈N*,使得Sn≥λ成立,
而Sn的最小值为1,
∴λ≤1…(12分)
∴an=n…(5分)
(Ⅱ)由(Ⅰ)得a1=1,a2=2,a3=3,a4=4
而{bn}是公比大于1的等比数列,
∴b1=1,b2=2,b3=4,∴q=2…(8分)
∴Sn=
| 1-2n |
| 1-2 |
又对任意n∈N*,使得Sn≥λ成立,
而Sn的最小值为1,
∴λ≤1…(12分)
点评:本题考查数列与方程、不等式交汇,考查等差、等比数列的定义和通项公式,等比数列的前n项和等知识,考查运算求解能力,考查化归与转化思想.

练习册系列答案
相关题目

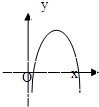
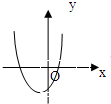
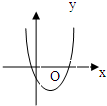
 已知函数f(x)=ax3+bx2+(c-3a-2b)x+d的图象如图所示.
已知函数f(x)=ax3+bx2+(c-3a-2b)x+d的图象如图所示.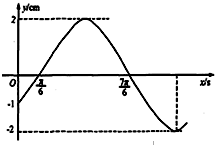 如图是某简谐运动的一段图象,其函数模型是f(x)=Asin(ωx+φ)(x≥0),其中A>0,ω>0,-
如图是某简谐运动的一段图象,其函数模型是f(x)=Asin(ωx+φ)(x≥0),其中A>0,ω>0,-