题目内容

已知tanα=-
3
4
，且α为第四象限角，则cosα等于（　　）
A、
3
5
B、-
3
5
C、
4
5
D、-
4
5
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：首先，根据1+tan2α=
1
cos2α
直接求解，然后，结合α为第四象限角进行进一步确定结果．
解答： 解：∵tanα=-
3
4
，且α为第四象限角，
∴cos2α=
1
1+tan2α
=
1
1+
9
16
=
16
25
，
∵α为第四象限角，
∴cosα=
4
5

故选：C．
点评：本题重点考查了同角三角函数基本关系式，属于基础题．
练习册系列答案
相关题目
集合A={x|x2-2x=0}B={-1，0，1}，则A∩B=（　　）
A、{0，2}B、{2}
C、{0}D、{0，1}
设Sn为等差数列{an}的前n项和，若a1=1，公差d=2，Sn+2-Sn=36，则n=（　　）
A、5B、6C、7D、8
已知二次函数f（x）=ax2+bx+c，其中abc＜0，则函数图象可能是（　　）
A、
B、
C、
D、
若角α的终边过点（-1，2），则cos2α的值为（　　）
A、
3
5
B、-
3
5
C、
5
5
D、-
5
5
已知0＜x＜1，0＜y＜1，求证：
x2+y2
+
x2+(1-y)2
+
(1-x)2+y2
+
(1-x)2+(1-y)2
≥2
2
．
2014年春节联欢晚会结束后，某网站就观众最喜欢的节目类型进行调查．
（Ⅰ）网站记者从现场观看晚会的5名观众A，B，C，D，E中随机抽取2人进行访谈，求观众A恰好被抽中的概率；
（Ⅱ）该网站又通过网络从观看电视直播的观众中选取1000名进行调查，经数据处理后得下列图表：

请你根据上述图表的数据信息，完成下列2×2列表的填写，并说明有多大的把握认为“是否最喜欢歌舞类节目和性别有关”
最喜欢歌舞类节目 不是最喜欢歌舞类节目 合计
男
女
合计 1000
下面的临界值表及公式可供参考：
P（K2≥k） 0.150 0.100 0.050 0.010 0.005 0.001
k 2.072 2.706 3.841 6.635 7.879 10.828
K2=
n(ad-bc)2
(a+b)(c+d)(a+c)(b+d)
，其中n=a+b+c+d．
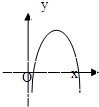
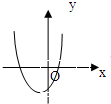
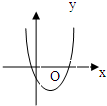
已知函数f（x）=ax3+bx2+（c-3a-2b）x+d的图象如图所示．
（1）求c，d的值；
（2）若函数f（x）在x=2处的切线方程为3x+y-11=0，求函数f（x）的解析式．
已知函数f（x）=3sin（ωx+φ）（ω＞0，-
π
2
＜φ＜0）的最小正周期为π，且其图象经过点（
2π
3
，0）．
（1）求函数f（x）的解析式；
（2）若函数g（x）=f（
x
2
+
5π
12
），α，β∈（0，π），且g（α）=1，g（β）=
3
2
4
，求g（α-β）的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网