题目内容
在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系.已知直线ρsin(θ+
)=0与曲线
(t为参数)无交点,则a的取值范围为 .
| π |
| 3 |
|
考点:简单曲线的极坐标方程,参数方程化成普通方程
专题:坐标系和参数方程
分析:直线ρsin(θ+
)=0展开化为y+
x=0,曲线
(t为参数)化为a2x2-y2=4.(a≠0).把y=-
x代入上述方程可得(a2-3)x2=4,因此当a2-3≤0时,上述方程无解,解得即可.
| π |
| 3 |
| 3 |
|
| 3 |
解答:
解:直线ρsin(θ+
)=0化为ρ•
sinθ+ρ•
cosθ=0,即y+
x=0.
曲线
(t为参数)化为a2x2-y2=4.(a≠0)
把y=-
x代入上述方程可得(a2-3)x2=4,
因此当a2-3≤0时,上述方程无解,解得-
≤a≤
且a≠0.
∴a的取值范围为[-
,0)∪(0,
].
故答案为:[-
,0)∪(0,
].
| π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
曲线
|
把y=-
| 3 |
因此当a2-3≤0时,上述方程无解,解得-
| 3 |
| 3 |
∴a的取值范围为[-
| 3 |
| 3 |
故答案为:[-
| 3 |
| 3 |
点评:本题考查了把极坐标方程化为直角坐标方程、参数方程化为普通方程、曲线的交点问题,考查了推理能力和计算能力,属于中档题.

练习册系列答案
相关题目
△ABC中,若
=
,则该三角形一定是( )
| a |
| cosB |
| b |
| cosA |
| A、等腰三角形但不是直角三角形 |
| B、直角三角形但不是等腰三角形 |
| C、等腰直角三角形 |
| D、等腰三角形或直角三角形 |
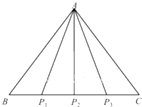 如图所示,△ABC是边长为1的正三角形,且点P在边BC上运动.当
如图所示,△ABC是边长为1的正三角形,且点P在边BC上运动.当