题目内容
对于空间中的三条直线，有以下四个条件：
①三条直线两两相交；
②三条直线两两平行；
③三条直线共点；
④两直线相交，第三条平行于其中一条与另个一条相交．
其中使这三条直线共面的充分条件有 个．
①三条直线两两相交；
②三条直线两两平行；
③三条直线共点；
④两直线相交，第三条平行于其中一条与另个一条相交．
其中使这三条直线共面的充分条件有
考点：空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：根据公理2以及推论进行判断，对于②③列举出三条直线两两平行在不同平面内的，三条相交直线不共面时，如三棱锥的侧面进行判断．
解答：
解：①中，如图①所示，由题意可设直线m与点A所确定的平面为α，则再由公理1，我们可以知道直线l、n也在α内．
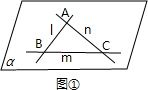
但三条直线为多面体过同一顶点的三条棱时，三条直线也两两相交，但三线不共面，
故①不满足要求，③不满足要求，
正方体的三条侧棱两两平行，但三线不共面，故②不满足要求，
④中，如图④所示，由题意可设直线m与直线n所确定的平面为α，则点A与点B均在平面α内，则再由公理1，我们可以知道直线l也在平面α内，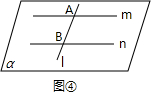
综合可得，④正确；
故答案为：1
但三条直线为多面体过同一顶点的三条棱时，三条直线也两两相交，但三线不共面，
故①不满足要求，③不满足要求，
正方体的三条侧棱两两平行，但三线不共面，故②不满足要求，
④中，如图④所示，由题意可设直线m与直线n所确定的平面为α，则点A与点B均在平面α内，则再由公理1，我们可以知道直线l也在平面α内，
综合可得，④正确；
故答案为：1
点评：数形结合是立体几何解题的常用方法，可以记住经常用到的哪些几何体例子．
练习册系列答案
名校课堂系列答案
相关题目
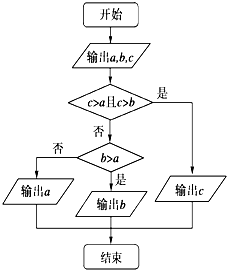如图程序框图表示的算法是（ ）| A、将a、b、c按从小到大输出 |
| B、将a、b、c按从大到小输出 |
| C、输出a、b、c三数中的最大数 |
| D、输出a、b、c三数中的最小数 |
对于函数f（x）=eax-lnx（a是实常数），下列结论正确的一个是（ ）
A、a=1时，f（x）有极大值，且极大值点x0∈（
| ||
B、a=2时，f（x）有极小值，且极小值点x0∈（0，
| ||
C、a=
| ||
| D、a＜0时，f（x）有极大值，且极大值点x0∈（-∞，0） |