题目内容
 如图所示,△ABC是边长为1的正三角形,且点P在边BC上运动.当
如图所示,△ABC是边长为1的正三角形,且点P在边BC上运动.当| PA |
| PC |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:如图所示,A(0,
),B(-
,0),C(
,0).设P(x,0),(-
≤x≤
).利用数量积和二次函数的单调性可得
•
(-x,
)•(
-x,0)=x2-
x=(x-
)2-
.当x=
时,当
•
取得最小值.再利用向量的夹角公式即可得出.
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| PA |
| PC |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 16 |
| 1 |
| 4 |
| PA |
| PC |
解答:
解:如图所示,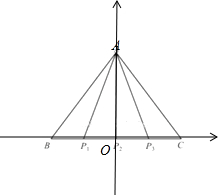
A(0,
),B(-
,0),C(
,0).
设P(x,0),(-
≤x≤
).
∴
•
(-x,
)•(
-x,0)=x2-
x=(x-
)2-
.
当x=
时,当
•
取得最小值.
此时
=(
,-
),
=(-
,-
),
•
=-
+
=
,
|
|=
=
,
∴cos∠PAB=
=
=
.
故答案为:
.

A(0,
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
设P(x,0),(-
| 1 |
| 2 |
| 1 |
| 2 |
∴
| PA |
| PC |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 16 |
当x=
| 1 |
| 4 |
| PA |
| PC |
此时
| AP |
| 1 |
| 4 |
| ||
| 2 |
| AB |
| 1 |
| 2 |
| ||
| 2 |
| AP |
| PB |
| 1 |
| 8 |
| 3 |
| 4 |
| 5 |
| 8 |
|
| AP |
(
|
| ||
| 4 |
∴cos∠PAB=
| ||||
|
|
| ||||
|
5
| ||
| 26 |
故答案为:
5
| ||
| 26 |
点评:本题考查了数量积和二次函数的单调性、向量的夹角公式,考查了推理能力和计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知i是虚数单位,则(1-i)(2+i)=( )
| A、-3-i | B、3-i |
| C、-3+i | D、3+i |
 如图,平面ABB1A1为圆柱OO1的轴截面,点C为
如图,平面ABB1A1为圆柱OO1的轴截面,点C为