题目内容
已知双曲线
+
=1的左、右焦点分别为F1、F2,以|F1F2|为直径的圆与双曲线渐近线的一个交点为(3,4),则此双曲线的方程为 .
| x2 |
| a2 |
| y2 |
| b2 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:根据题意,点(3,4)到原点的距离等于半焦距,可得a2+b2=25.由点(3,4)在双曲线的渐近线上,得到
=
,两式联解得出a=3且b=4,即可得到所求双曲线的方程.
| b |
| a |
| 4 |
| 3 |
解答:
解:∵点(3,4)在以|F1F2|为直径的圆上,
∴c=5,可得a2+b2=25…①
又∵点(3,4)在双曲线的渐近线y=
x上,
∴
=
…②,
①②联解,得a=3且b=4,可得双曲线的方程
-
=1.
故答案为:
-
=1.
∴c=5,可得a2+b2=25…①
又∵点(3,4)在双曲线的渐近线y=
| b |
| a |
∴
| b |
| a |
| 4 |
| 3 |
①②联解,得a=3且b=4,可得双曲线的方程
| x2 |
| 9 |
| y2 |
| 16 |
故答案为:
| x2 |
| 9 |
| y2 |
| 16 |
点评:本题给出双曲线满足的条件,求双曲线的方程,考查了双曲线的标准方程与简单几何性质等知识,属于中档题.

练习册系列答案
相关题目
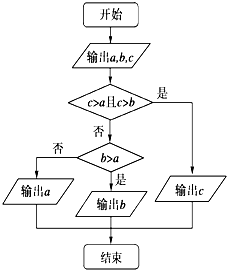 如图程序框图表示的算法是( )
如图程序框图表示的算法是( )| A、将a、b、c按从小到大输出 |
| B、将a、b、c按从大到小输出 |
| C、输出a、b、c三数中的最大数 |
| D、输出a、b、c三数中的最小数 |
已知i是虚数单位,则(1-i)(2+i)=( )
| A、-3-i | B、3-i |
| C、-3+i | D、3+i |
在极坐标系中,点P(4,
)到圆C:ρ=4cos(θ+
)上一点距离的最小值为( )
| 2π |
| 3 |
| π |
| 3 |
| A、8 | B、10 | C、4 | D、6 |