题目内容
1.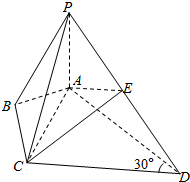 在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,E为PD的中点.
在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,E为PD的中点.(Ⅰ)求证:CE∥平面PAB;
(Ⅱ)当PA⊥CD,PA=AC,AB=1,PD=2$\sqrt{5}$时,求二面角P-CE-A的余弦值.
分析 (1)根据线面平行的判定定理进行证明即可;
(2)建立坐标系求出平面的法向量,利用向量法进行求解即可.
解答 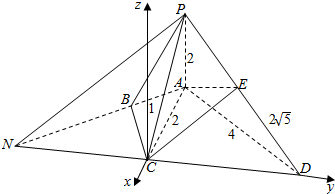 (1)证明:延长DC,AB交于点N,连PN.因为∠NAC=∠DAC,AC⊥CD,
(1)证明:延长DC,AB交于点N,连PN.因为∠NAC=∠DAC,AC⊥CD,
所以C为ND的中点.
而E为PD中点,所以EC∥PN.
因为EC?平面PAB,PN?平面PAB,
所以EC∥平面PAB.
(2)∵PA⊥CD,PA=AC,AB=1,PD=2$\sqrt{5}$,
∴AC=PC=2,AD=4,
则PA2+AD2=PD2,
即△PAD为直角三角形,
则PA⊥AD,
又∵CD∩AD=D,
∴PA⊥平面ACD,
以C为原点,以CA的反向延长线为x轴,CD为y轴,和PA平行的直线为z轴,
建立空间直角坐标系如图:
则C(0,0,0),A(-2,0,0),D(0,2$\sqrt{3}$,0),P(-2,0,2),E(-1,$\sqrt{3}$,1),
则$\overrightarrow{CD}$=(0,2$\sqrt{3}$,0),$\overrightarrow{CP}$=(-2,0,2),$\overrightarrow{CE}$=E(-1,$\sqrt{3}$,1),
设$\overrightarrow{n}$=(x,y,z)为面PCD的一个法向量,
则由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{CD}=0}\\{\overrightarrow{n}•\overrightarrow{CP}=0}\end{array}\right.$,得$\left\{\begin{array}{l}{2\sqrt{3}y=0}\\{-2x-2z=0}\end{array}\right.$,
得$\left\{\begin{array}{l}{y=0}\\{x+z=0}\end{array}\right.$,令x=1,则z=-1,
即$\overrightarrow{n}$=(1,0,-1),
设$\overrightarrow{m}$=(x,y,z)为面ACE的一个法向量,
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{CA}=0}\\{\overrightarrow{m}•\overrightarrow{CE}=0}\end{array}\right.$,得$\left\{\begin{array}{l}{-2x=0}\\{-x+\sqrt{3}y+z=0}\end{array}\right.$,即$\left\{\begin{array}{l}{x=0}\\{z=-\sqrt{3}y}\end{array}\right.$,
令y=1,则z=-$\sqrt{3}$,
则$\overrightarrow{m}$=(0,1,-$\sqrt{3}$)
∴cos<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{\sqrt{3}}{\sqrt{2}•\sqrt{1+3}}$=$\frac{\sqrt{3}}{2\sqrt{2}}$=$\frac{\sqrt{6}}{4}$,
即二面角P-CE-A的余弦值是$\frac{\sqrt{6}}{4}$.
点评 本题综合考查空间中线线面平行的判定和空间角的计算,涉及二面角的平面角,利用向量法是解决空间角常用的方法,考查的知识面较广,难度中等.

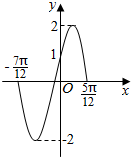
| A. | ω=2 | |
| B. | $f({\frac{π}{3}})=1$ | |
| C. | 函数f(x)的图象关于(-$\frac{11π}{12}$,0)对称 | |
| D. | 函数f(x)的图象向左平移$\frac{11π}{12}$个单位后得到y=Asinωx的图象 |
| A. | $\frac{1}{4}$ | B. | 0 | C. | -$\frac{3}{4}$ | D. | 1 |
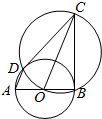 如图所示,直径分别为AB、OC的两圆相交于B、D两点,O为AB的中点.
如图所示,直径分别为AB、OC的两圆相交于B、D两点,O为AB的中点.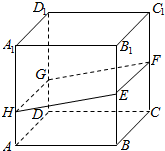 如图,边长为1的正方体ABCD-A1B1C1D1中,E、F分别为BB1、C1C的中点,DG=$\frac{1}{3}$DD1,过E、F、G的平面交AA1于点H,求A1D1到面EFGH的距离.
如图,边长为1的正方体ABCD-A1B1C1D1中,E、F分别为BB1、C1C的中点,DG=$\frac{1}{3}$DD1,过E、F、G的平面交AA1于点H,求A1D1到面EFGH的距离.