题目内容
16.已知函数f(x)的定义域为R,对任意实数x,y满足f(x+y)=f(x)+f(y)+$\frac{1}{2}$,且f($\frac{1}{2}$)=0.给出以下结论:①f(0)=-$\frac{1}{2}$;②f(-1)=-$\frac{3}{2}$;③f(x)为R上减函数;④f(x)+$\frac{1}{2}$为奇函数;
其中正确结论的序号是①②④.
分析 根据抽象函数的关系式,采用赋值法,可解决①②,在此基础上继续对各个选项逐一验证可得答案.
解答 解:①令x=y=0,
则f(0)=f(0)+f(0)+$\frac{1}{2}$,
即f(0)=-$\frac{1}{2}$,故①正确,
②令y=x=$\frac{1}{2}$,得f(1)=f($\frac{1}{2}$)+f($\frac{1}{2}$)+$\frac{1}{2}$=$\frac{1}{2}$;
令x=1,y=-1,得f(1-1)=f(1)+f(-1)+$\frac{1}{2}$=f(0),
即$\frac{1}{2}$+f(-1)+$\frac{1}{2}$=-$\frac{1}{2}$;
即f(-1)=-$\frac{3}{2}$,故②正确,
③取y=-1代入可得f(x-1)=f(x)+f(-1)+$\frac{1}{2}$,即f(x-1)-f(x)=f(-1)+$\frac{1}{2}$=-1<0,即f(x-1)<f(x),
故③f(x)为R上减函数,错误;
④令y=-x代入可-$\frac{1}{2}$=f(0)=f(x)+f(-x)+$\frac{1}{2}$,即f(x)+$\frac{1}{2}$+f(-x)+$\frac{1}{2}$=0,故f(x)+$\frac{1}{2}$为奇函数,故④正确,
故正确是①②④,
故答案为:①②④
点评 本题主要考查与函数有关的命题的真假判断,利用赋值法是解决抽象函数常用的一种方法,考查学生的运算和推理能力.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案
相关题目
9.已知函数f(x)=|2x-$\frac{a}{{2}^{x}}$|,其在区间[0,1]上单调递增,则a的取值范围为( )
| A. | [0,1] | B. | [-1,0] | C. | [-1,1] | D. | [-$\frac{1}{2}$,$\frac{1}{2}$] |
7.如果实数x,y满足条件$\left\{\begin{array}{l}{x-2y+2≥0}\\{2x-y-2≤0}\\{x+y-1≥0}\end{array}\right.$,則z=3x-2y的最小值为( )
| A. | -4 | B. | -2 | C. | 1 | D. | 2 |
4.已知点M(-4,0),N(4,0),B(2,0),动圆C与直线MN切于点B,过M、N与圆C相切的两直线相交于点P,则P点的轨迹方程是( )
| A. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1(x>2) | B. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1(x<-2) | ||
| C. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1(x≠±2) | D. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{12}$=1(x≠±2) |
11.集合A={1,3},B={1,2,3,4},则A∩B=( )
| A. | {1,2} | B. | {1,4} | C. | {1} | D. | {1,3} |
8.已知数列{an}的前n项和Sn=n2-2n+1,△ABC的三边长之比为a3:a4:a5,则△ABC的最大角的余弦值为( )
| A. | $\frac{\sqrt{2}-\sqrt{6}}{4}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{1}{4}$ | D. | -$\frac{\sqrt{3}}{2}$ |
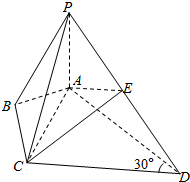 在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,E为PD的中点.
在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,E为PD的中点.