题目内容
9.设等差数列{an}的前n项和为Sn,且S4=4S2,a2+a4=10.(1)求数列{an}通项公式;
(2)若数列{bn}满足$\frac{{b}_{1}}{{a}_{1}}$+$\frac{{b}_{2}}{{a}_{2}}$+…+$\frac{{b}_{n}}{{a}_{n}}$=1-$\frac{1}{{2}^{n}}$,n∈N*,求数列{bn}的前n项和Tn.
分析 (1)通过设等差数列{an}的公差为d,利用等差中项及a2+a4=10可知a3=5,通过S4=4S2可知4a3-2d=4(2a3-3d),计算可得d=2,进而计算即得结论;
(2)通过$\frac{{b}_{1}}{{a}_{1}}$+$\frac{{b}_{2}}{{a}_{2}}$+…+$\frac{{b}_{n}}{{a}_{n}}$=1-$\frac{1}{{2}^{n}}$与$\frac{{b}_{1}}{{a}_{1}}$+$\frac{{b}_{2}}{{a}_{2}}$+…+$\frac{{b}_{n-1}}{{a}_{n-1}}$=1-$\frac{1}{{2}^{n-1}}$作差,结合(1)整理可知bn=$\frac{2n-1}{{2}^{n}}$(n≥2),验证当n=1时也成立,进而利用错位相减法计算即得结论.
解答 解:(1)设等差数列{an}的公差为d,
∵a2+a4=10,
∴a3=$\frac{{a}_{2}+{a}_{4}}{2}$=5,
∵S4=4S2,
∴4a3-2d=4(2a3-3d),
即20-2d=4(10-3d),解得:d=2,
∴an=a3+2(n-3)=2n-1;
(2)依题意,$\frac{{b}_{1}}{{a}_{1}}$+$\frac{{b}_{2}}{{a}_{2}}$+…+$\frac{{b}_{n}}{{a}_{n}}$=1-$\frac{1}{{2}^{n}}$,n∈N*,
当n≥2时,$\frac{{b}_{1}}{{a}_{1}}$+$\frac{{b}_{2}}{{a}_{2}}$+…+$\frac{{b}_{n-1}}{{a}_{n-1}}$=1-$\frac{1}{{2}^{n-1}}$,
两式相减得:$\frac{{b}_{n}}{{a}_{n}}$=(1-$\frac{1}{{2}^{n}}$)-(1-$\frac{1}{{2}^{n-1}}$)=$\frac{1}{{2}^{n}}$,
由(1)可知bn=$\frac{2n-1}{{2}^{n}}$(n≥2),
又∵b1=(1-$\frac{1}{2}$)a1=$\frac{1}{2}$满足上式,
∴bn=$\frac{2n-1}{{2}^{n}}$,n∈N*,
故Tn=$\frac{1}{2}$+$\frac{3}{{2}^{2}}$+…+$\frac{2n-1}{{2}^{n}}$,
$\frac{1}{2}$Tn=$\frac{1}{{2}^{2}}$+$\frac{3}{{2}^{3}}$+…+$\frac{2n-3}{{2}^{n}}$+$\frac{2n-1}{{2}^{n+1}}$,
两式相减得:$\frac{1}{2}$Tn=$\frac{1}{2}$+($\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n-1}}$)-$\frac{2n-1}{{2}^{n+1}}$
=$\frac{3}{2}$-$\frac{1}{{2}^{n-1}}$-$\frac{2n-1}{{2}^{n+1}}$,
∴Tn=3-$\frac{2n+3}{{2}^{n}}$.
点评 本题考查数列的通项及前n项和,考查错位相减法,考查运算求解能力,注意解题方法的积累,属于中档题.

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
| A. | 95 | B. | 94 | C. | 93 | D. | 92 |
| A. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1(x>2) | B. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1(x<-2) | ||
| C. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1(x≠±2) | D. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{12}$=1(x≠±2) |




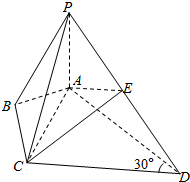 在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,E为PD的中点.
在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,E为PD的中点.