题目内容
如图，已知OPQ是半径为| 3 |
| π |
| 3 |
（Ⅰ）求函数f（x）的解析式，并写出其定义域；
（Ⅱ）求函数y=f（x）+f（x+
| π |
| 4 |
考点：三角函数的最值,三角函数中的恒等变换应用
专题：三角函数的图像与性质
分析：（1）先把矩形的各个边长用角x表示出来，进而表示出矩形的面积；
（2）先将函数y=f（x）+f（x+
）的解析式化为正弦型函数，进而根据正弦型函数的图象和性质得到答案．
（2）先将函数y=f（x）+f（x+
| π |
| 4 |
解答：
解：（1）在Rt△OBC中，OB=OC•cosx=
cosx，BC=OC•sinx=
sinx，
在Rt△OAD中，
=tan60°=
，
∴OA=
BC=sinx，
∵AB=OB-OA=
cosx-sinx，
∴f（x）=S=AB•BC=（
cosx-sinx）•
sinx
=3sinx•cosx-
sin2x
=
sin2x-
（1-cos2x）
=
sin（2x+
）-
，x∈（0，
）…（6分）
（Ⅱ）由x∈（0，
），x+
∈（0，
），得x∈（0，
）
而y=f（x）+f（x+
）=
sin（2x+
）-
+
sin[2（x+
）+
]-
=
[sin（2x+
）+cos（2x+
）]-
=
sin（2x+
）-
，
由2x+
∈（
，
），
故当2x+
=
，即x=
时，y取最大值
-
…（12分）
| 3 |
| 3 |
在Rt△OAD中，
| DA |
| OA |
| 3 |
∴OA=
| ||
| 3 |
∵AB=OB-OA=
| 3 |
∴f（x）=S=AB•BC=（
| 3 |
| 3 |
=3sinx•cosx-
| 3 |
=
| 3 |
| 2 |
| ||
| 2 |
=
| 3 |
| π |
| 6 |
| ||
| 2 |
| π |
| 3 |
（Ⅱ）由x∈（0，
| π |
| 3 |
| π |
| 4 |
| π |
| 3 |
| π |
| 12 |
而y=f（x）+f（x+
| π |
| 4 |
| 3 |
| π |
| 6 |
| ||
| 2 |
| 3 |
| π |
| 4 |
| π |
| 6 |
| ||
| 2 |
=
| 3 |
| π |
| 6 |
| π |
| 6 |
| 3 |
=
| 6 |
| 5π |
| 12 |
| 3 |
由2x+
| 5π |
| 12 |
| 5π |
| 12 |
| 7π |
| 12 |
故当2x+
| 5π |
| 12 |
| π |
| 2 |
| π |
| 24 |
| 6 |
| 3 |
点评：本题考查在实际问题中建立三角函数模型，解题关键是根据图形建立起三角模型，将三角模型用所学的恒等式变换公式进行化简，属于中档题．
练习册系列答案
相关题目
已知z（1+2i）=4+3i，则|z|=（ ）
A、
| ||
B、
| ||
| C、2 | ||
D、
|
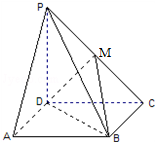在四棱锥P-ABCD中，侧棱PD⊥底面ABCD，底面ABCD是正方形，若PD=DA，M是PC的中点．