Question

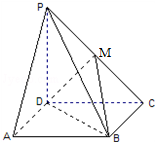在四棱锥P-ABCD中，侧棱PD⊥底面ABCD，底面ABCD是正方形，若PD=DA，M是PC的中点．
（Ⅰ）证明：PA∥平面BDM；
（Ⅱ）求二面角B-DM-C的余弦值．

Answer 1

考点：与二面角有关的立体几何综合题,直线与平面平行的判定

专题：空间角

分析：（Ⅰ）连结AC，交BD于O，连结MO，利用三角形的中位线推导出MO∥AP，由此能证明PA∥平面BDM．
（Ⅱ）以D原点，DA，DC，DP分别为x，y，z轴，建立空间直角坐标系，利用向量法能求出二面角B-DM-C的余弦值．

解答： （Ⅰ）证明：连结AC，交BD于O，连结MO，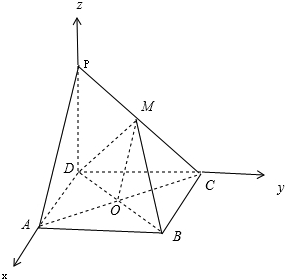
∵底面ABCD是正方形，M是PC的中点，
∴O是AC的中点，
∴MO是△APC的中位线，∴MO∥AP，
∵PA不包含于平面BDM，MO?平面BDM，
∴PA∥平面BDM．
（Ⅱ）解：以D原点，DA，DC，DP分别为x，y，z轴，
建立空间直角坐标系，
设PD=DA=2，∵侧棱PD⊥底面ABCD，底面ABCD是正方形，M是PC的中点，
∴D（0，0，0），B（2，2，0），C（0，2，0），P（0，0，2），M（0，1，1），
∴

DB

=(2，2，0)，

DM

=(0，1，1)，

DC

=（0，2，0），
设平面BDM的法向量

n

=(x，y，z)，则

n

•

DB

=0，

n

•

DM

=0，
∴

2x+2y=0 y+z=0

，取x=1，得

n

=（1，-1，1），
设平面DMC的法向量

m

=(x1，y1，z1)，则

m

•

DM

=0，

m

•

DC

=0，
∴

y1+z1=0 2y1=0

，∴

m

=（1，0，0），
设二面角B-DM-C的平面角为θ，
则cosθ=|cos＜

n

，

m

＞|=|

1

3

|=

3

3

．
∴二面角B-DM-C的余弦值是

3

3

．

点评：本题考查直线与平面平行的证明，考查二面角的余弦值的求法，解题时要认真审题，注意向量法的合理运用．