题目内容
3.设函数f(x)=sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$),给出以下四个论断:①它的周期为π;
②它的图象关于直线x=$\frac{π}{12}$对称;
③它的图象关于点($\frac{π}{3}$,0)对称;
④在区间(-$\frac{π}{6}$,0)上是增函数,
以其中两个论断为条件,另两个论断作结论,写出你认为正确的一个命题,条件①②结论③④.(注:填上你认为正确的一种答案即可)
分析 若 ①f(x)的周期为π,则 函数f(x)=sin(2x+φ),若再由②,可得φ=$\frac{π}{3}$,f(x)=sin(2x+$\frac{π}{3}$),显然能推出③④成立.
解答 解:若①f(x)的周期为π,则ω=2,函数f(x)=sin(2x+φ).
若再由②f(x)的图象关于直线x=$\frac{π}{12}$对称,则sin(2×$\frac{π}{12}$+φ) 取最值,
又∵-$\frac{π}{2}$<φ<$\frac{π}{2}$,
∴2×$\frac{π}{12}$+φ=$\frac{π}{2}$,
∴φ=$\frac{π}{3}$.
此时,f(x)=sin(2x+$\frac{π}{3}$),③④成立,
故由①②可以推出 ③④成立.
故答案为:①②,③④.另:①③⇒②④也正确.
点评 本题考查正弦函数的对称性,三角函数的周期性与求法,确定出函数的解析式,是解题的关键.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
18.“-2<m<-$\frac{1}{3}$”是“方程$\frac{{x}^{2}}{m+3}$+$\frac{{y}^{2}}{2m+1}$表示双曲线,且方程$\frac{{x}^{2}}{m+2}$-$\frac{{y}^{2}}{2m-1}$表示交点在y轴上的椭圆”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.函数f(x)=log2x+x-4的零点在区间为( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
12.已知直线l1的方程为Ax+3y+C=0,直线l2的方程为2x-3y+4=0,若l1与l2的交点在y轴上,则C的值为( )
| A. | 4 | B. | -4 | C. | ±4 | D. | 与A有关 |
13.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的焦点的渐近线的距离为2,且双曲线的一条渐近线与直线x-2y+3=0平行,则双曲线的方程为( )
| A. | $\frac{x^2}{16}-\frac{y^2}{4}=1$ | B. | $\frac{x^2}{9}-\frac{y^2}{4}=1$ | C. | $\frac{x^2}{4}-\frac{y^2}{9}=1$ | D. | $\frac{x^2}{8}-\frac{y^2}{4}=1$ |
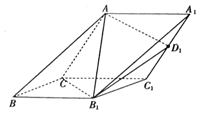 如图,在三棱柱ABC-A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠ACC1=∠CC1B1=60°,AC=2$\sqrt{3}$.
如图,在三棱柱ABC-A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠ACC1=∠CC1B1=60°,AC=2$\sqrt{3}$.