题目内容
9.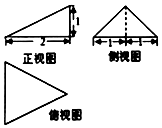 已知某三棱锥的三视图如图所示,则该三棱锥的体积为$\frac{2}{3}$,它的表面积为$2+2\sqrt{5}$.
已知某三棱锥的三视图如图所示,则该三棱锥的体积为$\frac{2}{3}$,它的表面积为$2+2\sqrt{5}$.
分析 由已知中的三视图,可得:该几何体是一个以俯视图为底面的三棱锥,代入锥体体积和表面积公式,可得答案.
解答 解:由已知中的三视图,可得:该几何体是一个以俯视图为底面的三棱锥,
其直观图如下图所示: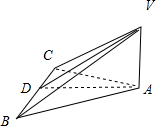
其底面ABC的面积为:$\frac{1}{2}$×2×2=2,
高VA=1,
故三棱锥的体积V=$\frac{2}{3}$,
AB=AC=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
故侧面VAB和VAC的面积均为:$\frac{1}{2}×\sqrt{5}×1$=$\frac{\sqrt{5}}{2}$,
侧面VBC的高VD=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
故侧面VBC的面积为:$\frac{1}{2}$×$2×\sqrt{5}$=$\sqrt{5}$,
故三棱锥的表面积为:$2+2\sqrt{5}$;
故答案为:$\frac{2}{3}$,$2+2\sqrt{5}$
点评 本题考查的知识点是棱锥的体积和表面积,简单几何体的三视图,难度中档.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
19.在极坐标系中,点(2,$\frac{2π}{3}$)到直线$ρsin(θ-\frac{π}{3})$=0的距离为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 3 |
18.“-2<m<-$\frac{1}{3}$”是“方程$\frac{{x}^{2}}{m+3}$+$\frac{{y}^{2}}{2m+1}$表示双曲线,且方程$\frac{{x}^{2}}{m+2}$-$\frac{{y}^{2}}{2m-1}$表示交点在y轴上的椭圆”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |