题目内容
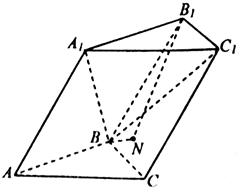 如图,三棱柱ABC-A1B1C1中,△ABC是正三角形,AA1=AB=2,平面ACC1A1⊥平面ABC,∠A1AC=60°.
如图,三棱柱ABC-A1B1C1中,△ABC是正三角形,AA1=AB=2,平面ACC1A1⊥平面ABC,∠A1AC=60°.(1)证明:A1B⊥AC;
(2)求二面角B-A1C1-C的余弦值;
(3)设点N是平面ACC1A1内的动点,求BN+B1N的最小值.
考点:用空间向量求平面间的夹角,直线与平面垂直的性质,点、线、面间的距离计算
专题:空间位置关系与距离,空间角
分析:(1)由已知条件推导出△A1AC是正三角形,取AC中点D,连结A1D、BD,能推导出AC⊥平面A1BD,由此能够证明A1B⊥AC.
(2)由已知条件推导出∠BA1D就是二面角B-A1C1-C的平面角,由此能求出二面角B-A1C1-C的余弦值;.
(3)以A为原点建立空间直角坐标系,利用向量法能求出BN+B1N的最小值.
(2)由已知条件推导出∠BA1D就是二面角B-A1C1-C的平面角,由此能求出二面角B-A1C1-C的余弦值;.
(3)以A为原点建立空间直角坐标系,利用向量法能求出BN+B1N的最小值.
解答:
(本小题满分14分)
(1)证明:∵AA1=AB=2,△ABC是正三角形,
∴AC=AB=2,
∴AA1=AC,
又∵∠A1AC=60°,
∴△A1AC是正三角形,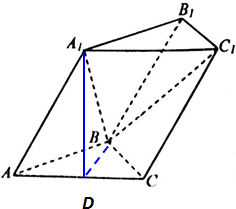
取AC中点D,连结A1D、BD,则A1D⊥AC,BD⊥AC
又∵A1D∩BD=D,A1D?平面A1BD,BD?平面A1BD,
∴AC⊥平面A1BD,
又∵A1B?平面A1BD,
∴A1B⊥AC.
(2)解:A1C1∥AC,由(1)知A1B⊥AC,A1D⊥AC,
∴A1B⊥A1C1,A1D⊥A1C1,
∴∠BA1D就是二面角B-A1C1-C的平面角;
∵平面ACC1A1⊥平面ABC,平面ACC1A1∩平面ABC=AC,
A1D?平面ACC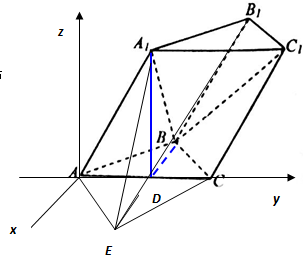 1A1,A1D⊥AC,
1A1,A1D⊥AC,
∴A1D⊥平面ABC.
∵BD?平面ABC,
∴A1D⊥BD.,
在Rt△A1BD 中, BD=
, A1D=
, A1B=
=
∴cos∠BA1D=
=
.
(3)解:延长BD至E使DE=BD,连结AE、CE、B1E,
则B1E就是BN+B1N的最小值,
以A为原点建立如图所示的空间直角坐标系,
则点E的坐标为(
, 1 , 0),
B1的坐标是(-
, 2 ,
),
∴B1E=
=4.
∴BN+B1N的最小值是4.
(1)证明:∵AA1=AB=2,△ABC是正三角形,
∴AC=AB=2,
∴AA1=AC,
又∵∠A1AC=60°,
∴△A1AC是正三角形,

取AC中点D,连结A1D、BD,则A1D⊥AC,BD⊥AC
又∵A1D∩BD=D,A1D?平面A1BD,BD?平面A1BD,
∴AC⊥平面A1BD,
又∵A1B?平面A1BD,
∴A1B⊥AC.
(2)解:A1C1∥AC,由(1)知A1B⊥AC,A1D⊥AC,
∴A1B⊥A1C1,A1D⊥A1C1,
∴∠BA1D就是二面角B-A1C1-C的平面角;
∵平面ACC1A1⊥平面ABC,平面ACC1A1∩平面ABC=AC,
A1D?平面ACC
 1A1,A1D⊥AC,
1A1,A1D⊥AC,∴A1D⊥平面ABC.
∵BD?平面ABC,
∴A1D⊥BD.,
在Rt△A1BD 中, BD=
| 3 |
| 3 |
| BD2+A1D2 |
| 6 |
∴cos∠BA1D=
| BD |
| A1B |
| ||
| 2 |
(3)解:延长BD至E使DE=BD,连结AE、CE、B1E,
则B1E就是BN+B1N的最小值,
以A为原点建立如图所示的空间直角坐标系,
则点E的坐标为(
| 3 |
B1的坐标是(-
| 3 |
| 3 |
∴B1E=
(-
|
∴BN+B1N的最小值是4.
点评:本题考查异面直线垂直的证明,考查二面角的余弦值的求法,考查两条线段和的最小值的求法,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
相关题目
在△ABC中,角A,B,C的对边分别a,b,c,若a2+b2=
c2.则直线ax-by+c=0被圆x2+y2=9所截得的弦长为( )
| 1 |
| 2 |
A、2
| ||
B、3
| ||
C、2
| ||
D、3
|