题目内容
设定圆M:(x+
)2+y2=16,动圆N过点F(
,0)且与圆M相切,记动圆N圆心N的轨迹为C.
(1)求轨迹C的方程;
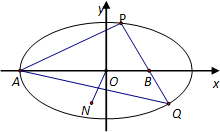
(2)已知A(-2,0),过定点B(1,0)的动直线l交轨迹C于P、Q两点,△APQ的外心为N.若直线l的斜率为k1,直线ON的斜率为k2,求证:k1•k2为定值.
| 3 |
| 3 |
(1)求轨迹C的方程;
(2)已知A(-2,0),过定点B(1,0)的动直线l交轨迹C于P、Q两点,△APQ的外心为N.若直线l的斜率为k1,直线ON的斜率为k2,求证:k1•k2为定值.
考点:直线与圆锥曲线的综合问题,轨迹方程
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知条件得圆N内切于圆M,|NM|+|NF|=4>|FM|,由此能求出点N的轨迹C的方程.
(2)设直线PQ为x=my+1设点P(x1,y1),Q(x2,y2),由
,得(m2+4)y2+2my-3=0,由此利用韦达定理综合已知条件能k1•k2为定值.
(2)设直线PQ为x=my+1设点P(x1,y1),Q(x2,y2),由
|
解答:
 (1)解:∵点F(
(1)解:∵点F(
,0)在圆M:(x+
)2+y2=16内,
∴圆N内切于圆M,
∴|NM|+|NF|=4>|FM|
∴点N的轨迹C的方程为
+y2=1.…(5分)
(2)证明:∵△APQ存在,
∴直线PQ斜率不为0
设直线PQ为x=my+1设点P(x1,y1),Q(x2,y2),
由
,得(m2+4)y2+2my-3=0,
,
直线AP的中垂线方程为:y=-
(x-
)+
,
即y=-
x+
+
,
∵
+4
=4,∴y=-
x-
,
∴y=-
x-
y1,∴y=-mx-
x-
,
同理得到直线AQ的中垂线方程为:y=-mx-
x-
,…(7分)
∴点N的坐标满足
,
∴
,
∴
,
∴
…(9分)
∴2y+2mx=-2mx-2mx,
解得k2=
=-3m
又∵直线l的斜率为k1,
∴k1=
(m≠0),∴k1k2=-3.…(13分)
 (1)解:∵点F(
(1)解:∵点F(| 3 |
| 3 |
∴圆N内切于圆M,
∴|NM|+|NF|=4>|FM|
∴点N的轨迹C的方程为
| x2 |
| 4 |
(2)证明:∵△APQ存在,
∴直线PQ斜率不为0
设直线PQ为x=my+1设点P(x1,y1),Q(x2,y2),
由
|
|
直线AP的中垂线方程为:y=-
| x1+2 |
| y1 |
| x1-2 |
| 2 |
| y1 |
| 2 |
即y=-
| x1+2 |
| y1 |
| ||
| 2y1 |
| y1 |
| 2 |
∵
| x | 2 1 |
| y | 2 1 |
| x1+2 |
| y1 |
| 3y1 |
| 2 |
∴y=-
| my1+3 |
| y1 |
| 3 |
| 2 |
| 2 |
| y1 |
| 3y1 |
| 2 |
同理得到直线AQ的中垂线方程为:y=-mx-
| 2 |
| y2 |
| 3y2 |
| 2 |
∴点N的坐标满足
|
∴
|
∴
|
∴
|
∴2y+2mx=-2mx-2mx,
解得k2=
| y |
| x |
又∵直线l的斜率为k1,
∴k1=
| 1 |
| m |
点评:本题考查轨迹方程的求法,考查斜率乘积为定值的证明,考查分析运算能力,考查推理论证能力,考查函数方程思想,考查分类整合思想,对数学思维能力的要求较高.

练习册系列答案
相关题目
执行如图所示的程序框图,输入的N=2014,则输出的S=( )


| A、2011 | B、2012 |
| C、2013 | D、2014 |
 如图,A、B是椭圆
如图,A、B是椭圆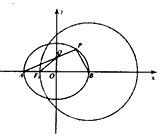 如图,点A,B分别是椭圆E:
如图,点A,B分别是椭圆E: