题目内容
14.已知函数f(x)=ax+$\frac{1}{x}$.(1)从区间(-2,2)内任取一个实数a,设事件A表示“函数y=f(x)-2在区间(0,+∞)上有两个不同的零点”,求事件A发生的概率;
(2)若连续掷两次一颗均匀的骰子(骰子六个面上标注的点数分别为1,2,3,4,5,6)得到的点数分别为a和b,记事件B表示“f(x)>b在x∈(0,+∞)上恒成立”,求事件B发生的概率.
分析 (1)由已知得ax2-2x+1=0有两个不同的正根x1和x2,由此利用根的判别式、韦达定理能求出0<a<1,由此能求出p(A).
(2)由已知a>0,x>0,所以f(x)>b,即ax2-bx+1>0在x∈(0,+∞)上恒成立,故需且只需△=b2-4a<0(*).由此利用列举法能求出事件B发生的概率P(B).
解答 解:(1)因为函数y=f(x)-2在区间(0,+∞)上有两个不同的零点,
所以f(x)-2=0,即ax2-2x+1=0有两个不同的正根x1和x2,
所以$\left\{\begin{array}{l}{a≠0}\\{{x}_{1}+{x}_{2}=\frac{2}{a}>0}\\{{x}_{1}{x}_{2}=\frac{1}{a}>0}\\{△=4-4a>0}\end{array}\right.$,解得0<a<1,所以p(A)=$\frac{1-0}{2-(-2)}$=$\frac{1}{4}$.
(2)由已知a>0,x>0,所以f(x)>b,即ax2-bx+1>0在x∈(0,+∞)上恒成立,
故需且只需△=b2-4a<0(*).
当a=1时,b=1适合(*);当a=2时,b=1,2适合(*);
当a=3,4时,b=1,2,3均适合(*);
当a=5,6时,b=1,2,3,4适合(*).
∴满足(*)的基本事件个数为m=1+2+6+8=17.
而基本事件总数为n=6×6=36,
所以事件B发生的概率P(B)=$\frac{m}{n}=\frac{17}{36}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意几何概型、列举法的合理运用.

练习册系列答案
相关题目
2.已知函数f(x)=$\left\{\begin{array}{l}{x,x≤0}\\{{x}^{2}-x,x>0}\end{array}\right.$,若函数g(x)=f(x)-m有三个不同的零点,则实数m的取值范围为( )
| A. | $({-\frac{1}{4},0})$ | B. | $({-\frac{1}{4},0}]$ | C. | $[{-\frac{1}{2},1}]$ | D. | $[{-\frac{1}{2},1})$ |
19.一个三角形的三个内角A,B,C成等差数列,则cosB=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
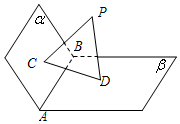 如图,已知平面α,β,且α∩β=AB,PC⊥α,PD⊥β,C,D是垂足.
如图,已知平面α,β,且α∩β=AB,PC⊥α,PD⊥β,C,D是垂足. 如图,公园有一块边长为2的等边三角形△ABC的地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
如图,公园有一块边长为2的等边三角形△ABC的地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.