一个三角形的三个内角A.B.C成等差数列.则cosB=( )A．$\frac{1}{2}$B．-$\frac{1}{2}$C．$\frac{\sqrt{3}}{2}$D．-$\frac{\sqrt{3}}{2}$ 题目和参考答案——青夏教育精英家教网—

题目内容

19．一个三角形的三个内角A，B，C成等差数列，则cosB=（　　）

A．

$\frac{1}{2}$

B．

-$\frac{1}{2}$

C．

$\frac{\sqrt{3}}{2}$

D．

-$\frac{\sqrt{3}}{2}$

分析直接由等差中项的概念结合三角形的内角和定理，特殊角的三角函数值可得答案．

解答解：∵三角形的三个内角A，B，C的度数成等差数列，
∴A+C=2B，
又A+C+B=180°，
∴3B=180°，
则B=60°．cosB=$\frac{1}{2}$．
故选：A．

点评本题考查了等差数列的性质，考查了三角形内角和定理，特殊角的三角函数值，是基础题．

练习册系列答案

相关题目

5．

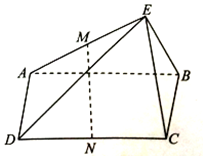如图，在四棱锥E-ABCD中，四边形ABCD为矩形，BC⊥EB，EA⊥EB，M，N分别为AE，CD的中点，求证：
（1）直线MN∥平面EBC；
（2）直线EA⊥平面EBC．

10．已知曲线$y=\frac{e}{x}$上一点P（1，e）处的切线分别交x轴、y轴于A，B两点，O为原点，则△OAB的面积为（　　）

e²

2e²

7．

如图，E，F，G分别是四面体ABCD的棱BC、CD、DA的中点，则此四面体与过E，F，G的截面平行的棱的条数是2．

14．已知函数f（x）=ax+$\frac{1}{x}$．
（1）从区间（-2，2）内任取一个实数a，设事件A表示“函数y=f（x）-2在区间（0，+∞）上有两个不同的零点”，求事件A发生的概率；
（2）若连续掷两次一颗均匀的骰子（骰子六个面上标注的点数分别为1，2，3，4，5，6）得到的点数分别为a和b，记事件B表示“f（x）＞b在x∈（0，+∞）上恒成立”，求事件B发生的概率．

4．函数f（x）=$\frac{{x}^{2}}{x-1}$（x＞1）的最小值为（　　）

11．向△ABC内任意投一点P，若△ABC面积为s，则△PBC的面积小于等于$\frac{s}{2}$的概率为$\frac{3}{4}$．

8．

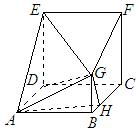在多面体ABCDEFG中，四边形ABCD与CDEF是边长均为a的正方形，CF⊥平面ABCD，BG⊥平面ABCD，H是BC上一点，且AB=2BG=4BH
（1）求证：平面AGH⊥平面EFG
（2）若a=4，求三棱锥G-ADE的体积．

9．已知向量$\overrightarrow{a}$=（1，1，0），$\overrightarrow b=（1，-2，2）$，且$k\overrightarrow a$与$\overrightarrow a+\overrightarrow b$互相垂直，则k的值为（　　）

试题分类