题目内容
20.已知盒子中有4个红球,2个白球,从中一次抓三个球,(1)求没有抓到白球的概率;
(2)记抓到球中的红球数为X,求X的分布列和数学期望.
分析 (1)使用组合数公式计算概率;
(2)根据超几何分布的概率公式计算概率,得出分布列,再计算数学期望.
解答 解:(1)没有抓到白球,即取到的全是红球,∴没有抓到白球的概率是$\frac{C_4^3C_2^0}{C_6^3}=\frac{1}{5}$.
(2)X的所有可能取值为1,2,3,
$P({X=1})=\frac{C_4^1C_2^2}{C_6^3}=\frac{1}{5}$,$P({X=2})=\frac{C_4^2C_2^1}{C_6^3}$=$\frac{3}{5}$,$P({X=3})=\frac{C_4^3C_2^0}{C_6^3}=\frac{1}{5}$,
∴X的分布列为:
| X | 1 | 2 | 3 |
| P | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
点评 本题考查了组合数公式,超几何分布,数学期望的计算,属于基础题.

练习册系列答案
相关题目
12.△ABC中,c是a与b的等差中项,sinA,sinB,sinC依次为一等比数列的前n项,前2n项,前3n项的和,则cosC的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{9}{16}$ | C. | $\frac{11}{16}$ | D. | $\frac{13}{16}$ |
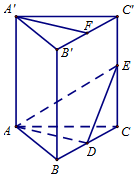 如图,在直三棱柱ABC-A'B'C'中,AB=AC,D、E分别是棱BC、CC'上的点(点D不同于点C),且AD⊥BC,F为B'C'的中点.求证:
如图,在直三棱柱ABC-A'B'C'中,AB=AC,D、E分别是棱BC、CC'上的点(点D不同于点C),且AD⊥BC,F为B'C'的中点.求证: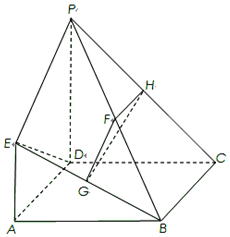 如图,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F,G,H分别为BP,BE,PC的中点.
如图,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F,G,H分别为BP,BE,PC的中点.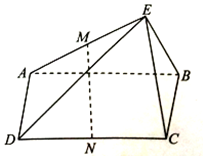 如图,在四棱锥E-ABCD中,四边形ABCD为矩形,BC⊥EB,EA⊥EB,M,N分别为AE,CD的中点,求证:
如图,在四棱锥E-ABCD中,四边形ABCD为矩形,BC⊥EB,EA⊥EB,M,N分别为AE,CD的中点,求证: