题目内容
9.已知x,y∈R,满足2≤y≤4-x,x≥1,则$\frac{{{x^2}+{y^2}+2x-2y+2}}{xy-x+y-1}$的最大值为$\frac{10}{3}$.分析 由已知不等式作出可行域,求得t=$\frac{y-1}{x+1}$的范围,把$\frac{{{x^2}+{y^2}+2x-2y+2}}{xy-x+y-1}$转化为含有t得代数式,再利用“对勾函数”的单调性求得答案.
解答 解:由2≤y≤4-x,x≥1,作出可行域如图,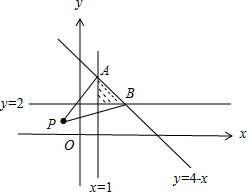
令t=$\frac{y-1}{x+1}$,其几何意义为可行域内的动点(x,y)与定点P(-1,1)连线的斜率,
联立$\left\{\begin{array}{l}{x=1}\\{y=4-x}\end{array}\right.$,解得A(1,3),
联立$\left\{\begin{array}{l}{y=2}\\{y=4-x}\end{array}\right.$,解得B(2,2).
∵${k}_{PA}=\frac{3-1}{1-(-1)}=1$,${k}_{PB}=\frac{2-1}{2-(-1)}=\frac{1}{3}$.
∴t∈[$\frac{1}{3}$,1].
$\frac{{x}^{2}+{y}^{2}+2x-2y+2}{xy-x+y-1}=\frac{(x+1)^{2}+(y-1)^{2}}{(x+1)(y-1)}$
=$\frac{x+1}{y-1}+\frac{y-1}{x+1}$=$\frac{1}{t}+t$.
设f(t)=$\frac{1}{t}+t$,则由“对勾函数”的单调性可知,f(t)=$\frac{1}{t}+t$在[$\frac{1}{3}$,1]上为减函数,
∴当t=$\frac{1}{3}$时,$f(x)_{max}=3+\frac{1}{3}=\frac{10}{3}$.
故答案为:$\frac{10}{3}$.
点评 本题考查函数的最值及其几何意义,考查简单的线性规划,训练了利用“对勾函数”的单调性求函数的最值,是中档题.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案| A. | -$\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | ±$\frac{4}{5}$ | D. | $\frac{3}{5}$ |
(Ⅰ)根据已知条件完成2×2列联表:
| 科幻片 | 文艺片 | 合计 | |
| 男 | |||
| 女 | |||
| 合计 |
随机变量${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$(其中n=a+b+c+d)
临界值表
| P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 25 | B. | 50 | C. | 100 | D. | 200 |
| 年龄(单位:岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 3 | 10 | 12 | 7 | 2 | 1 |
| 年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
| 赞成 | |||
| 不赞成 | |||
| 合计 |
| A. | $\frac{{4\sqrt{3}}}{5}$ | B. | $\frac{{3\sqrt{3}}}{5}$ | C. | $-\frac{{3\sqrt{3}}}{5}$ | D. | $-\frac{{4\sqrt{3}}}{5}$ |
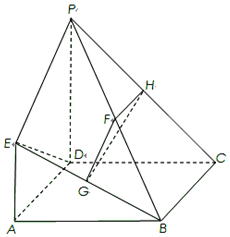 如图,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F,G,H分别为BP,BE,PC的中点.
如图,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F,G,H分别为BP,BE,PC的中点.