题目内容
4. 如图,公园有一块边长为2的等边三角形△ABC的地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
如图,公园有一块边长为2的等边三角形△ABC的地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.(1)设AD=x,DE=y,请将y表示为x的函数,并求出该函数的定义域;
(2)如果DE是灌溉水管,为节约成本,希望它最短,DE的位置应在哪里?如果DE是参观线路,则希望它最长,DE的位置又应在哪里?请予以说明.
分析 (1)利用三角形的面积公式得出AE与x的关系,再使用余弦定理得出y关于x的函数;
(2)利用基本不等式求y的最小值,利用函数单调性求y的最大值.
解答 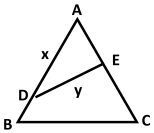 解:(1)在△ADE中,由余弦定理得:y2=x2+AE2-2x•AE•cos60°,
解:(1)在△ADE中,由余弦定理得:y2=x2+AE2-2x•AE•cos60°,
∴y2=x2+AE2-x•AE,①
又S△ADE=$\frac{1}{2}$AE•x•sin60°=$\frac{1}{2}$S△ABC=$\frac{\sqrt{3}}{2}$,∴x•AE=2,即AE=$\frac{2}{x}$,
∴${y^2}={x^2}+{(\frac{2}{x})^2}-2$(y>0),
∴$y=\sqrt{{x^2}+\frac{4}{x^2}-2}$.x∈[1,2].
(2)如果DE是水管,$y=\sqrt{{x^2}+\frac{4}{x^2}-2}≥\sqrt{2•2-2}=\sqrt{2}$
当且仅当${x^2}=\frac{4}{x^2}$,即$x=\sqrt{2}$时等号成立,
此时AD=DE=AE=$\sqrt{2}$.
如果DE是参观线路,记$f(x)={x^2}+\frac{4}{x^2}$-2,
则f(x)在$[1,\sqrt{2}]$上递减,在$[\sqrt{2},2]$上递增,
且f(1)=f(2)=3,
∴ymax=$\sqrt{3}$,此时DE为AB边的中线或AC边的中线.
点评 本题考查了函数最值的解法,函数单调性与基本不等式的应用,属于中档题.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
19.已知$cos(α-\frac{π}{3})=\frac{4}{5}$,则$sin(α+\frac{π}{3})+sinα$等于( )
| A. | $\frac{{4\sqrt{3}}}{5}$ | B. | $\frac{{3\sqrt{3}}}{5}$ | C. | $-\frac{{3\sqrt{3}}}{5}$ | D. | $-\frac{{4\sqrt{3}}}{5}$ |
16.已知数列{an},{bn}满足a1=$\frac{1}{2},{a_n}+{b_n}=1,{b_{n+1}}=\frac{b_n}{{1-{a_n}^2}}$,则b2017=( )
| A. | $\frac{2017}{2018}$ | B. | $\frac{2018}{2017}$ | C. | $\frac{2019}{2018}$ | D. | $\frac{2018}{2019}$ |
13.已知数列2008,2009,1,-2008,…若这个数列从第二项起,每一项都等于它的前后两项之和,则这个数列的前2017项之和S2017等于( )
| A. | 0 | B. | 2008 | C. | 2017 | D. | 4017 |