题目内容
证明：f（x）=x+
是奇函数．
| 4 |
| x |
考点：函数奇偶性的判断
专题：函数的性质及应用
分析：求函数的定义域，利用奇函数的定义即可得到结论．
解答：
解：要使函数有意义，则x≠0，
f（-x）=-x-
=-（x+
）=-f（x），
故f（x）=x+
是奇函数．
f（-x）=-x-
| 4 |
| x |
| 4 |
| x |
故f（x）=x+
| 4 |
| x |
点评：本题主要考查函数奇偶性的判断，根据奇函数的定义是解决本题的关键，比较基础．
练习册系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案
相关题目
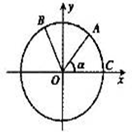如图，点A，B是单位圆O上的两点，点C是圆O与x轴正半轴的交点，将锐角α的终边OA按逆时针方向旋转
如图在四棱锥P一ABCD中，底面ABCD为直角梯形，AD∥BC，∠BAD=90°．BC=2AD，AC与BD交于点O，点M，N分别在线PC、AB上，