题目内容
(x2-
)9的展开式中x9的系数是 .
| 1 |
| 2x |
考点:二项式系数的性质
专题:二项式定理
分析:设所求系数为a,则存在非负整数r,使(-1)rC
•(
)rx18-3r=ax9成立,再由
,解得r的值,可得所求系数a的值.
r 9 |
| 1 |
| 2 |
|
解答:
解:设所求系数为a,则由二项展开式的通项公式知,存在非负整数r,
使C
(x2)9-r(-
)r=ax9,即(-1)rC
•(
)rx18-3r=ax9.
所以,得
,解得r=3,所求系数为a=-
C
=-
,
故答案为:-
.
使C
r 9 |
| 1 |
| 2x |
r 9 |
| 1 |
| 2 |
所以,得
|
| 1 |
| 8 |
3 9 |
| 21 |
| 2 |
故答案为:-
| 21 |
| 2 |
点评:本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于中档题.

练习册系列答案
相关题目
 如图在四棱锥P一ABCD中,底面ABCD为直角梯形,AD∥BC,∠BAD=90°.BC=2AD,AC与BD交于点O,点M,N分别在线PC、AB上,
如图在四棱锥P一ABCD中,底面ABCD为直角梯形,AD∥BC,∠BAD=90°.BC=2AD,AC与BD交于点O,点M,N分别在线PC、AB上,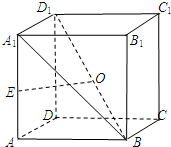 如图,在正方体ABCD-A1B1C1D1中,AA1=2,E为AA1的中点,O为BD1的中点.
如图,在正方体ABCD-A1B1C1D1中,AA1=2,E为AA1的中点,O为BD1的中点. 已知某四棱锥的三视图所示,其中俯视图和左视图都是腰长为4的等腰直角三角形,主视图为直角梯形,则几何体的体积是
已知某四棱锥的三视图所示,其中俯视图和左视图都是腰长为4的等腰直角三角形,主视图为直角梯形,则几何体的体积是