题目内容
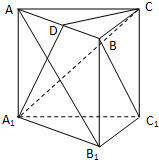 如图,已知直三棱柱ABC-A1B1C1中,AC⊥BC,D为AB的中点,AC=BC=BB1.
如图,已知直三棱柱ABC-A1B1C1中,AC⊥BC,D为AB的中点,AC=BC=BB1.(Ⅰ)求证:BC1∥平面CA1D;
(Ⅱ)求证:BC1⊥AB1.
考点:直线与平面平行的判定,空间中直线与直线之间的位置关系,直线与平面垂直的性质
专题:空间位置关系与距离
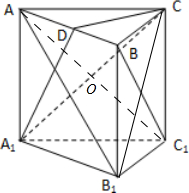
分析:(Ⅰ)连接AC1与CA1相交于O,连DO,根据已知可判断出AA1C1C是正方形,进而可知AO=OC1,又通过D为AB的中点,判断出OD∥BC1,利用线面判定定理证明出EF∥平面CA1D,
(Ⅱ)连接B1C,根据已知推断出BB1C1C是正方形,进而可知B1C⊥BC1,由因为AC⊥BC,且CC1⊥AC,推断出AC⊥平面BB1C1C,则AC⊥BC1,根据AC与B1C相交,进而判断出BC1⊥平面AB1C,最后利用线面垂直的性质可推断出BC1⊥AB1.
(Ⅱ)连接B1C,根据已知推断出BB1C1C是正方形,进而可知B1C⊥BC1,由因为AC⊥BC,且CC1⊥AC,推断出AC⊥平面BB1C1C,则AC⊥BC1,根据AC与B1C相交,进而判断出BC1⊥平面AB1C,最后利用线面垂直的性质可推断出BC1⊥AB1.
解答:
(Ⅰ)证明:连接AC1与CA1相交于O,连DO
∵AC=BC=BB1.
∴AA1C1C是正方形,
∴AO=OC1,
又∵D为AB的中点,
∴OD∥BC1,
∵BC1?平面CA1D,OD?平面CA1D,
∴BC1∥平面CA1D,
(Ⅱ)连接B1C,
∵BB1C1C是正方形,
∴B1C⊥BC1,
∵AC⊥BC,且CC1⊥AC,
∴AC⊥平面BB1C1C,
∴AC⊥BC1,
∵AC与B1C相交,
∴BC1⊥平面AB1C,
∴BC1⊥AB1.
∵AC=BC=BB1.
∴AA1C1C是正方形,
∴AO=OC1,
又∵D为AB的中点,
∴OD∥BC1,
∵BC1?平面CA1D,OD?平面CA1D,
∴BC1∥平面CA1D,
(Ⅱ)连接B1C,
∵BB1C1C是正方形,
∴B1C⊥BC1,
∵AC⊥BC,且CC1⊥AC,
∴AC⊥平面BB1C1C,
∴AC⊥BC1,
∵AC与B1C相交,
∴BC1⊥平面AB1C,
∴BC1⊥AB1.

点评:本题主要考查了线面平行的判定,线面垂直的性质等知识.注重了对学生基础知识的考查.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
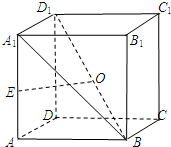 如图,在正方体ABCD-A1B1C1D1中,AA1=2,E为AA1的中点,O为BD1的中点.
如图,在正方体ABCD-A1B1C1D1中,AA1=2,E为AA1的中点,O为BD1的中点. 如图,已知AB是圆O的直径,圆O交BC于D,过点D作圆O的切线DE交AC于点E,且DE⊥AC.求证:AC=2OD.
如图,已知AB是圆O的直径,圆O交BC于D,过点D作圆O的切线DE交AC于点E,且DE⊥AC.求证:AC=2OD.