题目内容
若椭圆C1：
+
=1（a1＞b1＞0）和椭圆C2：
+
=1（a2＞b2＞0）的离心率相同，且a1＞a2，给出如下四个结论：
①椭圆C1和椭圆C2一定没有公共点；②
=
；③a12-a22＜b12-b22；④a1-a2＜b1-b2
则所有结论正确的序号是 ．
| x2 |
| a12 |
| y2 |
| b12 |
| x2 |
| a22 |
| y2 |
| b22 |
①椭圆C1和椭圆C2一定没有公共点；②
| a1 |
| a2 |
| b1 |
| b2 |
则所有结论正确的序号是
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：首先根据离心率相等可以进行恒等变换得到：②成立，同时得到a12-b12=a22-b22③不成立，①成立，最后利用（a1+b1）（a1-b1）=（a2+b2）（a2-b2）得到④成立．
解答：
解：椭圆C1：
+
=1（a1＞b1＞0）和椭圆C2：
+
=1（a2＞b2＞0）的离心率相同，
所以：a12-b12=a22-b22，
进一步转化为：a12-a22=b12-b22，
由于a1＞a2所以b1＞b2，
所以：①成立，
=
，
经过变换和合比性质得到：
=
，
所以：②成立．
a12-b12=a22-b22，所以：（a1+b1）（a1-b1）=（a2+b2）（a2-b2），
进一步得到：a1-a2＜b1-b2，故④成立．
故答案为：①②④．
| x2 |
| a12 |
| y2 |
| b12 |
| x2 |
| a22 |
| y2 |
| b22 |
所以：a12-b12=a22-b22，
进一步转化为：a12-a22=b12-b22，
由于a1＞a2所以b1＞b2，
所以：①成立，
| c1 |
| a1 |
| c2 |
| a2 |
经过变换和合比性质得到：
| a1 |
| a2 |
| b1 |
| b2 |
所以：②成立．
a12-b12=a22-b22，所以：（a1+b1）（a1-b1）=（a2+b2）（a2-b2），
进一步得到：a1-a2＜b1-b2，故④成立．
故答案为：①②④．
点评：本题考查的知识点：椭圆的性质的应用，不等式的应用，合比性质的应用，属于基础题型．
练习册系列答案
相关题目
集合A={x|-7＜x＜3}，集合B={x|1＜x＜7}，则A∪B=（ ）
| A、{x|-7＜x＜7} |
| B、{x|1＜x＜7} |
| C、{x|-7＜x＜3} |
| D、{x|1＜x＜3} |
已知A、B是x轴上的两点，点p的横坐标为3，且|PA|=|PB|，若直线PA的方程为x-2y+1=0，则直线PB的方程是（ ）
| A、2x+y+4=0 |
| B、2x+y-7=0 |
| C、x-2y+4=0 |
| D、x+2y-7=0 |
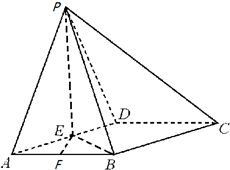如图所示，在四棱锥P-ABCD中，四边形ABCD为菱形，△PAD为正三角形，且E，F分别为AD，AB的中点，PE⊥平面ABCD，BE⊥平面PAD．