题目内容
已知A、B是x轴上的两点,点p的横坐标为3,且|PA|=|PB|,若直线PA的方程为x-2y+1=0,则直线PB的方程是( )
| A、2x+y+4=0 |
| B、2x+y-7=0 |
| C、x-2y+4=0 |
| D、x+2y-7=0 |
考点:直线的一般式方程
专题:直线与圆
分析:首先利用直线PA的方程为x-2y+1=0,和P点的横标求出点P的坐标,进一步利用中点求出A的坐标,根据P、A的坐标求出直线PA的方程.
解答:
解:已知点p的横坐标为3,点p在直线x-2y+1=0上,
所以:求得点p的纵标为:2,
所以:p(3,2),
直线PA的方程为x-2y+1=0,
则:A(-1,0),
由于|PA|=|PB|求出B(5,0),
根据p(3,2),B(7,0),
求得直线PB的方程为:x+2y-7=0.
故选:D.
所以:求得点p的纵标为:2,
所以:p(3,2),
直线PA的方程为x-2y+1=0,
则:A(-1,0),
由于|PA|=|PB|求出B(5,0),
根据p(3,2),B(7,0),
求得直线PB的方程为:x+2y-7=0.
故选:D.
点评:本题考查的知识要点:中点坐标的应用,利用点的坐标求直线的方程及相关的运算问题.

练习册系列答案
相关题目
若函数f(x)的定义域是[0,2],则函数g(x)=
的定义域是( )
| f(2x) |
| x-1 |
| A、[0,2] |
| B、(1,2] |
| C、[0,1) |
| D、以上都不对 |
“a=1”是“行列式
=0”的( )
|
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、非充分非必要条件 |
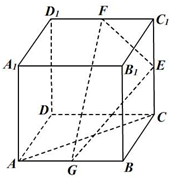 如图,棱长为2的正方体ABCD-A1B1C1D1中,点E,F,G分别为棱CC1,C1D1,AB的中点.
如图,棱长为2的正方体ABCD-A1B1C1D1中,点E,F,G分别为棱CC1,C1D1,AB的中点.