题目内容
推理三段论，“①修水一中号召全体学生学习雷锋做好事，要求每位学生至少做一件好事；②张三是修水一中高二年级学生；③所以张三必须至少做一件好事”中的“小前提”是（ ）
| A、① | B、② | C、①② | D、③ |
考点：演绎推理的基本方法
专题：规律型
分析：根据推理，确定三段论中的大前提；小前提；结论，从而可得结论．
解答：
解：大前提：①修水一中号召全体学生学习雷锋做好事，要求每位学生至少做一件好事；
小前提：②张三是修水一中高二年级学生；
结论：③所以张三必须至少做一件好事”；
故选：B
小前提：②张三是修水一中高二年级学生；
结论：③所以张三必须至少做一件好事”；
故选：B
点评：本题考查演绎推理的基本方法，考查三段论，属于基础题．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
设M（cos
x+cos
x，sin
x+sin
x）（x∈R）为坐标平面上一点，记f（x）=|
|2-2，且f（x）的图象与射线y=0（x≥0）交点的横坐标由小到大依次组成数列{an}，则|an+3-an|等于（ ）
| π |
| 3 |
| π |
| 4 |
| π |
| 3 |
| π |
| 4 |
| OM |
| A、12 | B、24 | C、36 | D、484 |
“x＞3”是“x2-5x+6＞0”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
圆x2+y2-2x=0的圆心坐标和半径分别为（ ）
| A、（1，0），1 |
| B、（0，1），1 |
| C、（-1，0），1 |
| D、（1，0），2 |
已知函数f（x）=x3，则下列说话正确的是（ ）
| A、f（x）为奇函数，且在（0，+∞）上是增函数 |
| B、f（x）为奇函数，且在（0，+∞）上是减函数 |
| C、f（x）为偶函数，且在（0，+∞）上是增函数 |
| D、f（x）为偶函数，且在（0，+∞）上是偶函数 |
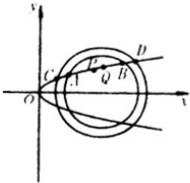如图所示，设抛物线y2=2px，（0＜p＜1）与圆（x-5）2+y2=9在x轴上方的交点为A、B，与圆（x-6）2+y2=27在x轴上方的交点为C、D，P为AB中点，Q为CD的中点．