题目内容
数列{an}满足3an=2Sn+3,n∈N*
(Ⅰ) 求a1及数列{an}的通项公式;
(Ⅱ) 令bn=
(n∈N*),求数列{bn}的前n项和Sn.
(Ⅰ) 求a1及数列{an}的通项公式;
(Ⅱ) 令bn=
| 1 |
| (log3an)•(log3an+1) |
考点:数列的求和,等比关系的确定
专题:等差数列与等比数列
分析:(Ⅰ)由已知知条件推导出3a1=2a1+3,解得a1=3.n≥2时,an=Sn-Sn-1=
an-
an-1,由此求出an=3n.
(Ⅱ)bn=
=
=
-
,由此利用裂项求法能求出数列{bn}的前n项和Sn.
| 3 |
| 2 |
| 3 |
| 2 |
(Ⅱ)bn=
| 1 |
| (log3an)•(log3an+1) |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
解答:
解:(Ⅰ)∵数列{an}满足3an=2Sn+3,n∈N*,
∴n=1时,3a1=2a1+3,解得a1=3.
n≥2时,Sn=
an-
,Sn-1=
an-1-
,
an=Sn-Sn-1=
an-
an-1,
整理,得an=3an-1,
∴数列{an}是等比数列,公比为3,首项为3,
∴an=3n.
(Ⅱ)bn=
=
=
-
,
∴Sn=1-
+
-
+…+
-
=1-
=
.
∴n=1时,3a1=2a1+3,解得a1=3.
n≥2时,Sn=
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
an=Sn-Sn-1=
| 3 |
| 2 |
| 3 |
| 2 |
整理,得an=3an-1,
∴数列{an}是等比数列,公比为3,首项为3,
∴an=3n.
(Ⅱ)bn=
| 1 |
| (log3an)•(log3an+1) |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴Sn=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
=1-
| 1 |
| n+1 |
=
| n |
| n+1 |
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,解题时要认真审题,注意裂项求和法的合理运用.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
已知函数f(x)x∈(a,b)的导函数为f′(x),原命题为“若f′(x)<0,则f(x)在(a,b)上单调递减”,关于其逆命题、否命题、逆否命题真假性的判断依次如下,正确的是( )
| A、真,真,真 |
| B、假,假,假 |
| C、真,真,假 |
| D、假,假,真 |
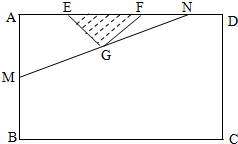 某小区想利用一矩形空地ABCD建市民健身广场,设计时决定保留空地边上的一水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中AD=60m,AB=40m,且△EFG中,∠EGF=90°,经测量得到AE=10m,EF=20m.为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点G作一直线交AB,DF于M,N,从而得到五边形MBCDN的市民健身广场,设DN=x(m).
某小区想利用一矩形空地ABCD建市民健身广场,设计时决定保留空地边上的一水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中AD=60m,AB=40m,且△EFG中,∠EGF=90°,经测量得到AE=10m,EF=20m.为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点G作一直线交AB,DF于M,N,从而得到五边形MBCDN的市民健身广场,设DN=x(m).