题目内容
已知正项等比数列{an}满足a2014=a2013+2a2012,且
=4a1,则6(
+
)的最小值为( )
| anam |
| 1 |
| m |
| 1 |
| n |
A、
| ||
| B、2 | ||
| C、4 | ||
| D、6 |
考点:等比数列的性质
专题:计算题,等差数列与等比数列
分析:由已知可解得数列的公比q,进而可得n+m=6,代入要求的式子由基本不等式可得.
解答:
解:设正项等比数列{an}的公比为q,q>0
∵a2014=a2013+2a2012,
∴a2012q2=a2012q+2a2012,
同除以a2012可得q2-q-2=0,
解得q=2,或q=-1(舍去),
又∵
=4a1,
∴an•am=a12•2n+m-2=16a12,
∴2n+m-2=16=24,
∴n+m-2=4,
变形可得n+m=6,
∴6(
+
)=(m+n)(
+
)=2+
+
≥2+2
=4,
当且仅当
=
,即m=n=3时取等号,
故选:C.
∵a2014=a2013+2a2012,
∴a2012q2=a2012q+2a2012,
同除以a2012可得q2-q-2=0,
解得q=2,或q=-1(舍去),
又∵
| anam |
∴an•am=a12•2n+m-2=16a12,
∴2n+m-2=16=24,
∴n+m-2=4,
变形可得n+m=6,
∴6(
| 1 |
| m |
| 1 |
| n |
| 1 |
| m |
| 1 |
| n |
| n |
| m |
| m |
| n |
≥2+2
|
当且仅当
| n |
| m |
| m |
| n |
故选:C.
点评:本题考查等比数列的性质,涉及基本不等式的应用,属中档题.

练习册系列答案
相关题目
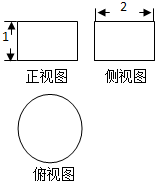 如图所示,一个空间几何体的正视图和侧视图都是相邻两边的长分别为1和2的矩形,俯视图是一个圆,那么这个几何体的体积为( )
如图所示,一个空间几何体的正视图和侧视图都是相邻两边的长分别为1和2的矩形,俯视图是一个圆,那么这个几何体的体积为( )| A、4π | ||
| B、π | ||
C、
| ||
D、
|
已知抛物线C1:x2=2y的焦点为F,以F为圆心的圆C2交C1于A,B两点,交C1的准线于C,D两点,若四边形ABCD是矩形,则圆C2的方程为( )
| A、x2+(y-1)2=12 | ||
| B、x2+(y-1)2=16 | ||
C、x2+(y-
| ||
D、x2+(y-
|
定义在R上的函数f(x)满足:对任意α,β∈R,总有f(α+β)-[f(α)+f(β)]=2014,则下列说法正确的是( )
| A、f(x)+1是奇函数 |
| B、f(x)-1是奇函数 |
| C、f(x)+2014是奇函数 |
| D、f(x)-2014是奇函数 |
若点O和点F分别为椭圆
+y2=1的中心和左焦点,点P为椭圆上的任意一点,则
•
的最大值为( )
| x2 |
| 2 |
| OP |
| FP |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列函数中,既是奇函数,又在(0,+∞)上是减函数的是( )
A、y=
| ||
| B、y=x2 | ||
| C、y=x | ||
| D、y=-x+1 |