题目内容
设M(cos
x+cos
x,sin
x+sin
x)(x∈R)为坐标平面上一点,记f(x)=|
|2-2,且f(x)的图象与射线y=0(x≥0)交点的横坐标由小到大依次组成数列{an},则|an+3-an|等于( )
| π |
| 3 |
| π |
| 4 |
| π |
| 3 |
| π |
| 4 |
| OM |
| A、12 | B、24 | C、36 | D、484 |
考点:数列与函数的综合,数列与向量的综合
专题:等差数列与等比数列,三角函数的求值
分析:先求出f(x)的函数表达式,在令f(x)=0,所求出的x的解即为与x轴的交点,在选出其非负值,即为{an}的项.
解答:
解:f(x)=(cos
x+cos
x)2+(sin
x+sin
x)2-2
=2cos(
x)
∴f(x)与x轴的非负半轴的交点为:
x=kπ+
,k∈{0,1,2,3,…}
∴x=6+12k,k∈{0,1,2,3,…}
∴交点的横坐标由小到大依次组成数列{an}的通项公式为:
an=6+12(n-1),n∈{0,1,2,3,…}
∴|an+3-an|=12×3=36
故答案为:36
| π |
| 3 |
| π |
| 4 |
| π |
| 3 |
| π |
| 4 |
=2cos(
| π |
| 12 |
∴f(x)与x轴的非负半轴的交点为:
| π |
| 12 |
| π |
| 2 |
∴x=6+12k,k∈{0,1,2,3,…}
∴交点的横坐标由小到大依次组成数列{an}的通项公式为:
an=6+12(n-1),n∈{0,1,2,3,…}
∴|an+3-an|=12×3=36
故答案为:36
点评:本题考察了函数与数列的结合,一般解题思路是先根据函数找出数列的通项公式,其要注意的点就是数列的项数是非负的,注意区别函数的定义域.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
已知函数h(x)=x2+px+q在(n,n+1)(n∈Z)有两个不同零点,令A=max{h(n),h(n+1)},B=min{h(n),h(n+1)},(其中max表示两个数中较大的,而min表示两个数中较小的),则( )
A、B<
| ||||
B、B>
| ||||
C、B<
| ||||
D、B>
|
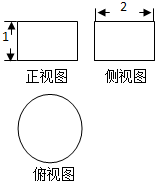 如图所示,一个空间几何体的正视图和侧视图都是相邻两边的长分别为1和2的矩形,俯视图是一个圆,那么这个几何体的体积为( )
如图所示,一个空间几何体的正视图和侧视图都是相邻两边的长分别为1和2的矩形,俯视图是一个圆,那么这个几何体的体积为( )| A、4π | ||
| B、π | ||
C、
| ||
D、
|
一平面截球O得到半径为
cm的圆面,球心到这个平面的距离是2cm,则球O的体积是( )
| 5 |
| A、12πcm3 | ||
| B、36πcm3 | ||
C、64
| ||
| D、108πcm3 |
若θ∈[
,
],sin2θ=
,则sinθ=( )
| π |
| 4 |
| π |
| 2 |
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知函数f(x)x∈(a,b)的导函数为f′(x),原命题为“若f′(x)<0,则f(x)在(a,b)上单调递减”,关于其逆命题、否命题、逆否命题真假性的判断依次如下,正确的是( )
| A、真,真,真 |
| B、假,假,假 |
| C、真,真,假 |
| D、假,假,真 |