题目内容
已知
=（cos
，sin
），
=（cos
，-sin
），其中x∈[-
，
]．求证：（
+
）⊥(
-
)．
| a |
| 3x |
| 2 |
| 3x |
| 2 |
| b |
| x |
| 2 |
| x |
| 2 |
| π |
| 2 |
| π |
| 2 |
| a |
| b |
| a |
| b |
考点：平面向量数量积的运算
专题：证明题,三角函数的求值,平面向量及应用
分析：分别求得向量a，b的模，再由向量垂直的条件即为数量积为0，即可得证．
解答：
证明：由于
=（cos
，sin
），
=（cos
，-sin
），
则|
|=
=1，|
|=
=1，
则有（
+
）•（
-
）=
2-
2=1-1=0，
则（
+
）⊥(
-
)．
| a |
| 3x |
| 2 |
| 3x |
| 2 |
| b |
| x |
| 2 |
| x |
| 2 |
则|
| a |
cos2
|
| b |
cos2
|
则有（
| a |
| b |
| a |
| b |
| a |
| b |
则（
| a |
| b |
| a |
| b |
点评：本题考查平面向量的数量积的性质，考查向量的垂直的条件即为数量积为0，考查运算能力，属于基础题．
练习册系列答案
相关题目
设t∈R，m，n都是不为1的正数，函数f（x）=mx+t•nx若m=2，n=
，且t≠0，请判断函数y=f（x）的图象是否具有对称性，如果具有，请求出对称轴方程或对称中心坐标；若不具有，请说明理由．
| 1 |
| 2 |
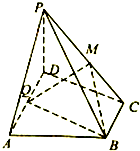如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，AD||BC，PD⊥底面ABCD，