题目内容

若f（x）是以
π
2
为周期的函数，且f（
π
3
）=1，则f（-
2π
3
）=
 
．
考点：函数的周期性
专题：函数的性质及应用
分析：由
π
2
为函数周期，可得π为函数周期，然后由f（-
2π
3
）=f（-
2π
3
+π）=f（
π
3
）得答案．
解答： 解：∵f（x）是以
π
2
为周期的函数，且f（
π
3
）=1，
∴f（-
2π
3
）=f（-
2π
3
+π）=f（
π
3
）=1．
故答案为：1．
点评：本题考查了函数的周期，若非0常数T为函数的周期，则T的所有非0整数倍都是函数的周期，是基础题．
练习册系列答案
相关题目
下列问题不是解决问题的算法的是（　　）
A、方程x2-4x+3=0有两个不等的实根
B、解一元一次方程的步骤是去分母、去括号、移项、合并同类项、化系数为1
C、从中山到北京先坐汽车，再坐火车
D、解不等式ax+3＞0时，第一步移项，第二步讨论
过抛物线y2=4x的焦点焦点F作倾斜角为α的直线，交抛物线于A（x1，y1），B（x2，y2）两点，
（1）若α=45°，求线段AB的中点C到抛物线准线的距离；
（2）求证：y1y2=-4．
从坐标原点O作曲线y=lnx的切线OP（P为切点），再过切点P引切线的垂线L，L与y轴的交点为Q．
（Ⅰ）求点P及点Q的坐标；
（Ⅱ）证明：点P是曲线y=lnx上距离点Q最近的点．
已知函数f（x）=|x-a|+|x-1|，a∈R．
（1）当a=3时，解不等式f（x）≤4；
（2）当x∈（-2，1）时，f（x）＞|2x-a-1|，求a的取值范围．
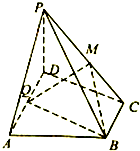如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，AD||BC，PD⊥底面ABCD，∠ADC=90°，BC=
1
2
AD=1，PD=CD=2，Q为AD的中点，M为棱PC上一点．
（Ⅰ）试确定点M的位置，使得PA||平面BMQ，并证明你的结论；
（Ⅱ）若PM=2MC，求二面角P-BQ-M的余弦值．
已知函数f（x）=ax+2ln（ax+1），其中实常a∈（1，6）．
（Ⅰ）当a=2时，比较f（x）与6x2+6x的大小；
（Ⅱ）已知函数f（x）的图象与直线y=6x相切，证明x∈（1，3）时，（x+3）f（
x
-1
2
）＜6x-6．
对于给定数列{cn}，如果存在实常数p，q使得cn+1=pcn+q对于任意n∈N*都成立，我们称数列{cn}是“线性数列”．
（1）若an=2n，bn=3•2n，n∈N*，数列{an}、{bn}是否为“线性数列”？若是，指出它对应的实常数p&，q，若不是，请说明理由；
（2）证明：若数列{an}是“线性数列”，则数列{an+an+1}也是“线性数列”；
（3）若数列{an}满足a1=2，an+an+1=3t•2n（n∈N*），t为常数．求数列{an}前n项的和．
已知函数f（x）=x2+mx-2n，m，n∈[0，2]，则使f（1）≤0成立的概率是（　　）
A、
1
4
B、
1
2
C、
3
8
D、
5
8

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网