题目内容
下列命题错误的是( )
| A、命题“若m>0,则方程x2+x-m=0有实根”的逆否命题为:“若方程x2+x-m=0无实根,则m≤0”; | ||||||||||||||||
| B、“x=1”是“x2-3x+2=0”的充分不必要条件; | ||||||||||||||||
| C、命题p:?x0∈R,|sinx0|>1,则¬p:对?x∈R,|sinx|≤1; | ||||||||||||||||
D、命题“若
|
考点:命题的真假判断与应用
专题:简易逻辑
分析:A.利用逆否命题的定义即可判断出;
B.由x2-3x+2=0解得x=1,2,即可“x=1”是“x2-3x+2=0”的充分不必要;
C.利用¬p的定义即可得出;
D.利用命题的否定定义只否定结论即可判断出.
B.由x2-3x+2=0解得x=1,2,即可“x=1”是“x2-3x+2=0”的充分不必要;
C.利用¬p的定义即可得出;
D.利用命题的否定定义只否定结论即可判断出.
解答:
解:A.命题“若m>0,则方程x2+x-m=0有实根”的逆否命题为:“若方程x2+x-m=0无实根,则m≤0”,正确;
B.由x2-3x+2=0解得x=1,2,∴“x=1”是“x2-3x+2=0”的充分不必要,正确;
C.命题p:?x0∈R,|sinx0|>1,则¬p:对?x∈R,|sinx|≤1,正确;
D.命题“若
•
=0,则
、
中至少有一个为零向量”的否定是:“若
•
=0,则
、
都不为零向量”,因此不正确.
故选:D.
B.由x2-3x+2=0解得x=1,2,∴“x=1”是“x2-3x+2=0”的充分不必要,正确;
C.命题p:?x0∈R,|sinx0|>1,则¬p:对?x∈R,|sinx|≤1,正确;
D.命题“若
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
故选:D.
点评:本题考查了简易逻辑的判定,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)=x2+mx-2n,m,n∈[0,2],则使f(1)≤0成立的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
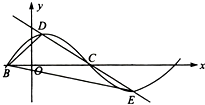 已知函数f(x)=Asin(πx+φ)的部分图象如图所示,点B,C是该图象与x轴的交点,过点C的直线与该图象交于D,E两点,则(
已知函数f(x)=Asin(πx+φ)的部分图象如图所示,点B,C是该图象与x轴的交点,过点C的直线与该图象交于D,E两点,则(| BD |
| BE |
| BE |
| CE |
| A、-1 | ||
B、-
| ||
C、
| ||
| D、2 |
已知函数f(x)=
,如果f(x0)=2,那么实数x0的值为( )
|
| A、4 | B、0 | C、1或4 | D、1或-2 |
sin
的值为( )
| 11π |
| 6 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|