题目内容
19.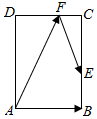 如图,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,点E在边BC上,点F在边CD上,若$\overrightarrow{DF}$=λ$\overrightarrow{DC}$,$\overrightarrow{CE}$=λ2$\overrightarrow{CB}$,则$\overrightarrow{AF}$•$\overrightarrow{FE}$的最大值为$\frac{1}{6}$.
如图,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,点E在边BC上,点F在边CD上,若$\overrightarrow{DF}$=λ$\overrightarrow{DC}$,$\overrightarrow{CE}$=λ2$\overrightarrow{CB}$,则$\overrightarrow{AF}$•$\overrightarrow{FE}$的最大值为$\frac{1}{6}$.
分析 以A为坐标原点,AB所在直线为x轴,AD所在直线为y轴,建立直角坐标系,可得A(0,0),B($\sqrt{2}$,0),C($\sqrt{2}$,2),D(0,2),设E($\sqrt{2}$,n),F(m,2),运用向量共线的坐标表示,解得m,n,再由向量的数量积的坐标表示,结合二次函数的最值的求法,即可得到最大值.
解答 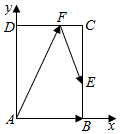 解:以A为坐标原点,AB所在直线为x轴,AD所在直线为y轴,建立直角坐标系,
解:以A为坐标原点,AB所在直线为x轴,AD所在直线为y轴,建立直角坐标系,
可得A(0,0),B($\sqrt{2}$,0),C($\sqrt{2}$,2),D(0,2),
设E($\sqrt{2}$,n),F(m,2),
由$\overrightarrow{DF}$=λ$\overrightarrow{DC}$,可得m=$\sqrt{2}$λ,即F($\sqrt{2}$λ,2),
由$\overrightarrow{CE}$=λ2$\overrightarrow{CB}$,可得n=2-2λ2,即E($\sqrt{2}$,2-2λ2),
则$\overrightarrow{AF}$•$\overrightarrow{FE}$=($\sqrt{2}$λ,2)•($\sqrt{2}$-$\sqrt{2}$λ,-2λ2)
=2λ(1-λ)-4λ2=-6λ2+2λ=-6(λ-$\frac{1}{6}$)2+$\frac{1}{6}$,
当λ=$\frac{1}{6}$时,则$\overrightarrow{AF}$•$\overrightarrow{FE}$取得最大值$\frac{1}{6}$.
故答案为:$\frac{1}{6}$.
点评 本题考查向量的数量积的最值的求法,注意运用坐标法,考查二次函数的最值的求法,以及化简运算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.若集合$M=\left\{{x∈R\left|{\frac{x+2}{x-1}≤0}\right.}\right\}{,_{\;}}N$为自然数集,则下列选项正确的是( )
| A. | M⊆{x|x≥1} | B. | M⊆{x|x>-2} | C. | M∩N={0} | D. | M∪N=N |
7.已知数列{an}满足an+1+an=n,若a1=2,则a8-a4=( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
14.已知a,b,c∈R,则“a>0且b2-4ac<0”是“?x∈R,都有ax2+bx+c≥0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
11.某程序框图如图所示,则该程序运行后输出的值是( )


| A. | 2014 | B. | 2015 | C. | 2016 | D. | 2017 |
9.设集合M={x|x2-2x<0},N={x|y=lg(4-x2)},则( )
| A. | M∪N=M | B. | (∁RM)∩N=R | C. | (∁RM)∩N=∅ | D. | M∩N=M |
