题目内容
8.定义在R上的函数f(x)满足f(x)=$\left\{\begin{array}{l}{lo{g}_{3}(2-x)(x≤0)}\\{f(x-1)-f(x-2)(x>0)}\end{array}\right.$,则f(2016)的值为log32.分析 由f(x)=f(x-1)-f(x-2)推导可得f(x)=-f(x-3)=f(x-6),从而解得.
解答 解:∵f(x)=f(x-1)-f(x-2)
=f(x-2)-f(x-3)-f(x-2)=-f(x-3),
∴f(x)=-f(x-3)=f(x-6),
故f(2016)=f(336•6)=f(0)=llog3(2-0)=log32,
故答案为:log32.
点评 本题考查了学生的化简运算能力及函数的性质的判断与应用.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
3.二项式(1-x)6的展开式中x2的系数是( )
| A. | -20 | B. | -15 | C. | 15 | D. | 20 |
13.下列有关命题的说法错误的是( )
| A. | 若“p∨q”为假命题,则p,q均为假命题 | |
| B. | “x=1”是“x≥1”的充分不必要条件 | |
| C. | 若命题p:?x0∈R,x${\;}_{0}^{2}$≥0,则命题¬p:?x∈R,x2<0 | |
| D. | “sinx=$\frac{1}{2}$”的必要不充分条件是“x=$\frac{π}{6}$” |
18.已知z=2+i,(i是虚数单位),z的共轭复数是$\overline z$,则复数$\frac{\overline z}{i}$=( )
| A. | -1-2i | B. | 1-2i | C. | -1+2i | D. | 1+2i |
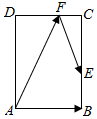 如图,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,点E在边BC上,点F在边CD上,若$\overrightarrow{DF}$=λ$\overrightarrow{DC}$,$\overrightarrow{CE}$=λ2$\overrightarrow{CB}$,则$\overrightarrow{AF}$•$\overrightarrow{FE}$的最大值为$\frac{1}{6}$.
如图,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,点E在边BC上,点F在边CD上,若$\overrightarrow{DF}$=λ$\overrightarrow{DC}$,$\overrightarrow{CE}$=λ2$\overrightarrow{CB}$,则$\overrightarrow{AF}$•$\overrightarrow{FE}$的最大值为$\frac{1}{6}$.