题目内容
10.若集合$M=\left\{{x∈R\left|{\frac{x+2}{x-1}≤0}\right.}\right\}{,_{\;}}N$为自然数集,则下列选项正确的是( )| A. | M⊆{x|x≥1} | B. | M⊆{x|x>-2} | C. | M∩N={0} | D. | M∪N=N |
分析 解分式不等式求出集合M,进而逐一分析四个答案的正误,可得结论.
解答 解:∵$M=\left\{x∈R|\frac{x+2}{x-1}≤0\right\}$=[-2,1),
N为自然数集,
故M⊆{x|x≥1}错误;
M⊆{x|x>-2}错误;
M∩N={0}正确;
M∪N=N错误;
故选:C.
点评 本题考查的知识点是集合的包含关系的判断与应用,集合的交集,并集运算,难度不大,属于基础题.

练习册系列答案
相关题目
20.在等差数列{an}中,a3+a5=12-a7,则a1+a9=( )
| A. | 8 | B. | 12 | C. | 16 | D. | 20 |
1.已知θ∈(0,$\frac{π}{4}$),且sinθ-cosθ=-$\frac{\sqrt{14}}{4}$,则$\frac{2co{s}^{2}θ-1}{cos(\frac{π}{4}+θ)}$等于( )
| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{2}$ |
5.执行如图的程序框图,则输出S的值为( )


| A. | 2 | B. | -3 | C. | $-\frac{1}{2}$ | D. | $\frac{1}{3}$ |
15.某校组织由5名学生参加的演讲比赛,采用抽签法决定演讲顺序,在“学生A和B都不是第一个出场,B不是最后一个出场”的前提下,学生C第一个出场的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{9}$ | D. | $\frac{3}{20}$ |
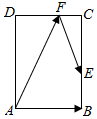 如图,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,点E在边BC上,点F在边CD上,若$\overrightarrow{DF}$=λ$\overrightarrow{DC}$,$\overrightarrow{CE}$=λ2$\overrightarrow{CB}$,则$\overrightarrow{AF}$•$\overrightarrow{FE}$的最大值为$\frac{1}{6}$.
如图,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,点E在边BC上,点F在边CD上,若$\overrightarrow{DF}$=λ$\overrightarrow{DC}$,$\overrightarrow{CE}$=λ2$\overrightarrow{CB}$,则$\overrightarrow{AF}$•$\overrightarrow{FE}$的最大值为$\frac{1}{6}$.